关系数据库中的事务故障恢复并不是一个新问题,自70年代关系数据库诞生之后就一直伴随着数据库技术的发展,并且在分布式数据库的场景下又遇到了一些新的问题。本文将会就事务故障恢复这个问题,分别讲述单机数据库、分布式数据库中遇到的问题和几种典型的解决方案,以及 OceanBase 在事务故障恢复方面的相关实践。
分布式系统
分布式系统 分类中有 8 篇文章
超越不可能
相信所有研究过分布式系统的同学都对大名鼎鼎的FLP不可能性有所耳闻,简单来说,FLP不可能性证明了“在可能有哪怕一个进程故障的异步系统模型中,共识问题无法被解决”。但矛盾的是,现在正当红的很多分布式系统,都依赖于底层的共识算法,比如Multi-Paxos、Raft等,难道是FLP错了么?共识问题已经被解决了?还是说我们用的分布式系统都是有问题的?
想要理解这个问题,其实是要搞清楚一件事情:FLP不可能性真正意味着什么?
注:如无特殊说明,本文中的进程故障模型均为crash-stop,通信链路模型为perfect link。
Paxos与“幽灵复现”
Paxos被公认是难度很高的分布式共识算法,一方面是体现在理解其算法正确性的难度上,而另一方,体现在工程实现的复杂度上。在将Paxos算法运用在工程实践的过程会遇到各种各样的问题,本文要探讨的“幽灵复现”问题,就是其中一例。
什么是“幽灵复现”
据我所知,所谓的“幽灵复现”问题是Oceanbase团队在实现Multi-Paxos过程中自己提出的,并随着郁白的一篇知名博文的传播被大家所知晓。这里先简单介绍一下问题场景:
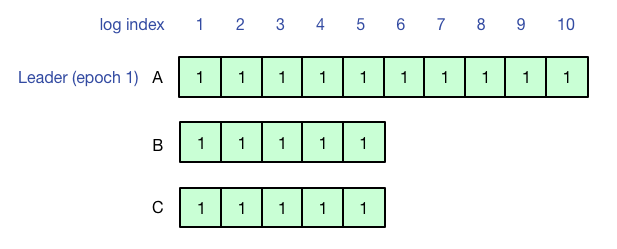
使用有Leader lease(避免活锁,leader读写提供线性一致性)的Multi-Paxos来实现复制状态机,刚开始A是Leader,客户端执行操作写1-10号日志,1-5号日志形成多数派,但是6-10号日志没有同步到其他副本,客户端超时。
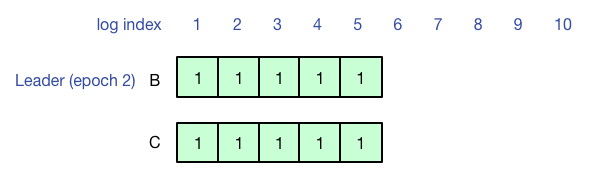
之后A宕机,B成为新的Leader,由于联系不到A,B和C作为多数派从6号日志开始工作,此时查询不到先前客户端在A上写的结果(6-10号日志没有同步成功)。
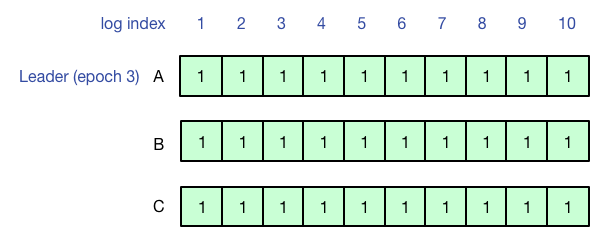
最后A再次成为Leader,并成功把之前的6-10号日志同步到多数派,此时再查询,就可以查询到之前客户端写入的结果了。
[paper note]Megastore & PaxosStore
之前对分布式KV存储关注不多,最近抽时间看了一下Google的Megastore和Wechat的PaxosStore的论文,发现其中很多设计考量的角度都很有趣,值得仔细思考。
Megastore
Megastore相对来说是一个比较老的系统了,是在Spanner大规模运用之前构建在Bigtable之上,支持跨行事务的一套过渡解决方案。
结构
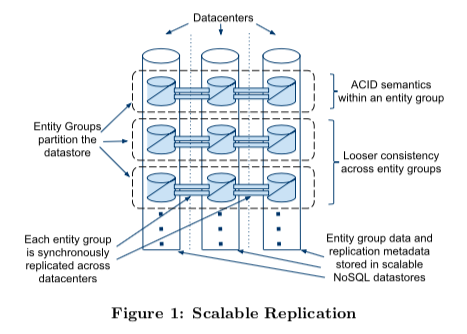
整体上来看,Megastore把和root table中某个root entity相关的所有child table中的行组成一个entity group,并以此作为多副本同步的基本单元。在设计上通过切分entity group,将绝大部分访问限制在entity group内部获得了扩展性的提高,再通过Paxos对entity group做多副本,获得了可用性的提高。
[paper note]Consensus on Transaction Commit
这篇论文的作者实在太吓人了,Jim Gray和Leslie Lamport,两个领域的扛把子。论文介绍的内容叫Paxos Commit,是用分布式共识算法解决分布式事务的原子提交问题,不愧是这两位大佬写出来的文章哈哈。
PS:这篇文章是我的paper note,主要是帮助自己理解和记忆,与其说是文章,其实更像是简单的笔记。
解决了什么问题
事务的属性是ACID,A代表原子性,事务要么全部提交,要么全部失败,不能出现提交了一半的情况。单机事务的原子性通过日志系统来保证,而在分布式事务里,通常的做法是两阶段提交(Tow Phase Commit,2PC)。
两阶段提交的一个重要问题是协调者宕机问题,参与者执行完Prepare状态后,参与者处于“未决”状态,意味着参与者自己无法决定事务状态,而如果此时协调者宕机,事务的状态将无法推进下去。
Paxos Commit希望解决这个问题,即在事务提交过程中,能够容忍F个副本失败而不会导致事务无法推进。
另外,论文中还提到了其他尝试解决此问题的方法(三阶段提交),并表示不屑一顾……….(三阶段提交实际上并没有改善提交过程的容灾)
Paxos revisit
前一段时间借着组里的实习生学习交流的机会,又重新讨论了一次Paxos算法,颇有收获。本文整理记录几个我个人觉得比较有意义的问题,希望通过思考这几个问题,能够加深你对Paxos算法的理解。
本文假定读者已经对Paxos算法有一定了解(包括原理、正确性证明、执行流程),如果你还不了解Paxos,请移步这里。
Paxos算法流程
在思考问题之前,首先重温一下Paxos算法的流程,同时统一变量名称,方便后文讨论。
Prepare阶段:
- Proposer选择proposal number n,并向acceptors发送Prepare(n)消息
- Acceptor收到Prepare(n):if n > minProposal then minProposal = n; return (acceptedProposal, acceptedValue)
Accept阶段:
- 如果Proposer收到了超过多数派acceptors对于Prepare(n)的回复,如果回复中有包含acceptedValue,则选择acceptedProposal值最大的作为value,否则Proposer可以自行选择value
- Proposer向所有acceptors发出Accept(n, value)消息
- Acceptor收到Accept(n, value):if n >= minProposal then acceptedProposal = n; acceptedValue = value,并回复AcceptAck(n)
- Proposer收到来自多数派acceptors的AcceptAck消息,value已达成决议(chosen)
问题
在上述Paxos算法流程的基础上,仔细思考下面几个问题:
- 为了保证算法在容灾(节点故障重启)场景下的正确性,Acceptor上需要持久化哪些信息?
-
如果Acceptor不持久化acceptedProposal,在Prepare阶段的第2步中minProposal代替,有没有问题?
-
Accept阶段,Proposer不用n覆盖acceptedProposal,仍将其发送给Acceptor,Acceptor收到Accept(n, acceptedProposal, value)之后使用消息中的acceptedProposal而不是n来作为acceptedProposal,有没有问题?
-
在5个节点的情况下,如果修改流程为Proposer要收到4个acceptor对Prepare(n)的回应才可以发送Accept消息,要收到2个acceptor对Accept(n, value)的回应才能确认决议,有没有问题?
-
论文中提到Proposer选择proposal number要递增且不重复,这个要求是不是必要的?如果把Prepare阶段第2步中的>改为>=呢?
WARNING: 强烈建议花一些来仔细思考上面的问题,在得出自己的答案之后再继续往下看
被误用的“一致性”
想必每个接触过分布式系统的同学都没少看到过“一致性”这个词,但是我最近有一个越来越强烈的感觉:“一致性”这个词已经被严重的误用了,以至于当我看到这个词的时候,我甚至得花些功夫去思考这到底指的是哪个“一致性”,更严重的是,当别人在谈到“一致性”的时候,实际上他们在谈的完全是另一种东西。
无辜的Paxos
故事的起因来源于Paxos(没错,又是这货),网上对于Paxos的文献太多,而且质量参差不齐,在绝大多数的中文文档中,你都可以看到这样的描述:“Paxos是一个分布式强一致性协议”,不瞒你说,每次看到这样的表述的时候,我的内心是崩溃的…且听我慢慢道来。
问题的由来很大一部分原因在于英文对中文的翻译,因此我们必须将术语还原到英文进行讨论,『一致性』对应的英文名词应该是Consistency没错了,然后我们在Lamport大神的原始论文《Paxos Made Simple》中搜索关键词,你会发现:
没错,论文中一次都没有提到过Consistency,也就是说,Paxos和『一致性』根本半毛钱关系都没有啊!那Paxos究竟是什么呢?论文中写的很明确——”The Consensus Algorithm”。
PS:本文中所有使用中文“一致”均指Consistency,“共识”为Consensus。
分布式共识(Consensus):Viewstamped Replication、Raft以及Paxos
从上篇文章到现在,已经有半年多的时间没有写过什么了,时间真是匆匆而过,感觉从上次写博客到现在似乎也就是一眨眼的功夫。
回顾我这大半年,完全可以用四个字概括:“不务正业”,先是跟着曼昆的书学习了微观、宏观经济学的基础知识,恶补了一下个人理财的基础理论(很有意思,但依然挡不住我买的基金嗷嗷跌),然后又入坑了摄影(其实就是买个微单瞎拍瞎修)。至于个人的技术提升方面就显得捉襟见肘了,先是跟着斯坦福CS145、CS245两门课程复习了一下数据库方面的知识,然后就在分布式系统的泥沼中挣扎到了现在…可能唯一一件值得纪念的事情就是去年年底抱大牛大腿参加某司举办的hackathon,过程中学到了一点Golang的皮毛,最后搞了个apple watch耍(队友大牛依然表示对结果不太满意…),另外出于对tby大牛的仰慕,又补习了一下前端开发技能,然并卵,已经又忘光了…
一不小心写了一大段流水账,回归主题。之前花了大概两个多月时间从头琢磨分布式系统,研一时候修这门课完全是白学了,本来学的就不好,两年过去基本也不剩什么了。翻了两本最出名的教材,看了一些高校的课程安排和slides,总算感觉自己有点“上道”了~
这篇文章主要总结一下我个人认为是整个分布式系统中最为重要的问题(没有之一):分布式共识(Consensus)。
PS:我在学习过程中是以《分布式系统:概念与设计》1这本书作为基础的,在下文中如果没有特别指明,所提书中内容均指该书。