关系数据库中的事务故障恢复并不是一个新问题,自70年代关系数据库诞生之后就一直伴随着数据库技术的发展,并且在分布式数据库的场景下又遇到了一些新的问题。本文将会就事务故障恢复这个问题,分别讲述单机数据库、分布式数据库中遇到的问题和几种典型的解决方案,以及 OceanBase 在事务故障恢复方面的相关实践。
超越不可能
相信所有研究过分布式系统的同学都对大名鼎鼎的FLP不可能性有所耳闻,简单来说,FLP不可能性证明了“在可能有哪怕一个进程故障的异步系统模型中,共识问题无法被解决”。但矛盾的是,现在正当红的很多分布式系统,都依赖于底层的共识算法,比如Multi-Paxos、Raft等,难道是FLP错了么?共识问题已经被解决了?还是说我们用的分布式系统都是有问题的?
想要理解这个问题,其实是要搞清楚一件事情:FLP不可能性真正意味着什么?
注:如无特殊说明,本文中的进程故障模型均为crash-stop,通信链路模型为perfect link。
可串行化(Serializable):理想和现实
但凡是接触过数据库的同学一定不会对事务(transaction)的概念感到陌生,我第一次接触事务的概念还是在本科的数据库课本上,了解了事务并发控制概念,但在之后多年不严肃的前后台开发经历中,我几乎从来没有考虑过数据库的“隔离级别”,这让我产生了一种”数据库如此好用,世界如此美好“的幻觉…直到现在从事了数据库内核的开发工作,才对事务的并发控制有了一点点认真的理解。
这篇文章即是我对事务并发控制的一些粗浅的理解。
事务并发执行的正确性
一般来说,教科书中都是类似的描述事务:”数据库并发控制的基本单元“,事务管理器和执行引擎需要和并发控制协作,来保证数据库中事务的执行是”正确“的。数据库中事务并发控制的正确性,也就是我们常说的Isolation。
PS:并发事务的正确性除了我们最常讨论的Isolation之外还有Consistency和Recoverable,限于篇幅,本文仅讨论Isolation。
Paxos与“幽灵复现”
Paxos被公认是难度很高的分布式共识算法,一方面是体现在理解其算法正确性的难度上,而另一方,体现在工程实现的复杂度上。在将Paxos算法运用在工程实践的过程会遇到各种各样的问题,本文要探讨的“幽灵复现”问题,就是其中一例。
什么是“幽灵复现”
据我所知,所谓的“幽灵复现”问题是Oceanbase团队在实现Multi-Paxos过程中自己提出的,并随着郁白的一篇知名博文的传播被大家所知晓。这里先简单介绍一下问题场景:
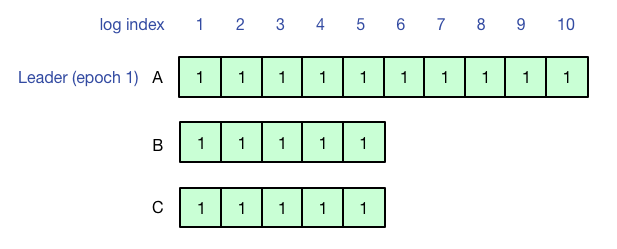
使用有Leader lease(避免活锁,leader读写提供线性一致性)的Multi-Paxos来实现复制状态机,刚开始A是Leader,客户端执行操作写1-10号日志,1-5号日志形成多数派,但是6-10号日志没有同步到其他副本,客户端超时。
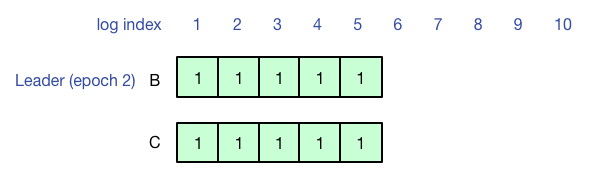
之后A宕机,B成为新的Leader,由于联系不到A,B和C作为多数派从6号日志开始工作,此时查询不到先前客户端在A上写的结果(6-10号日志没有同步成功)。
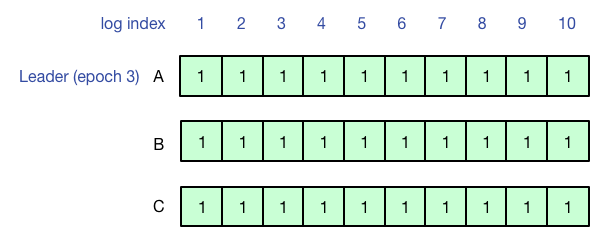
最后A再次成为Leader,并成功把之前的6-10号日志同步到多数派,此时再查询,就可以查询到之前客户端写入的结果了。
[paper note]Megastore & PaxosStore
之前对分布式KV存储关注不多,最近抽时间看了一下Google的Megastore和Wechat的PaxosStore的论文,发现其中很多设计考量的角度都很有趣,值得仔细思考。
Megastore
Megastore相对来说是一个比较老的系统了,是在Spanner大规模运用之前构建在Bigtable之上,支持跨行事务的一套过渡解决方案。
结构
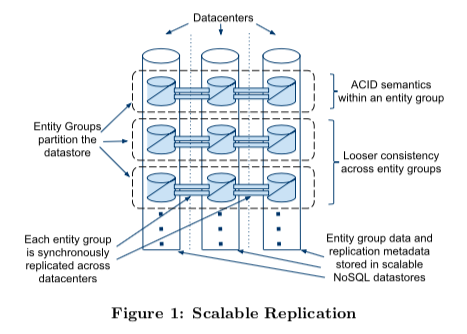
整体上来看,Megastore把和root table中某个root entity相关的所有child table中的行组成一个entity group,并以此作为多副本同步的基本单元。在设计上通过切分entity group,将绝大部分访问限制在entity group内部获得了扩展性的提高,再通过Paxos对entity group做多副本,获得了可用性的提高。
[paper note]Consensus on Transaction Commit
这篇论文的作者实在太吓人了,Jim Gray和Leslie Lamport,两个领域的扛把子。论文介绍的内容叫Paxos Commit,是用分布式共识算法解决分布式事务的原子提交问题,不愧是这两位大佬写出来的文章哈哈。
PS:这篇文章是我的paper note,主要是帮助自己理解和记忆,与其说是文章,其实更像是简单的笔记。
解决了什么问题
事务的属性是ACID,A代表原子性,事务要么全部提交,要么全部失败,不能出现提交了一半的情况。单机事务的原子性通过日志系统来保证,而在分布式事务里,通常的做法是两阶段提交(Tow Phase Commit,2PC)。
两阶段提交的一个重要问题是协调者宕机问题,参与者执行完Prepare状态后,参与者处于“未决”状态,意味着参与者自己无法决定事务状态,而如果此时协调者宕机,事务的状态将无法推进下去。
Paxos Commit希望解决这个问题,即在事务提交过程中,能够容忍F个副本失败而不会导致事务无法推进。
另外,论文中还提到了其他尝试解决此问题的方法(三阶段提交),并表示不屑一顾……….(三阶段提交实际上并没有改善提交过程的容灾)
Paxos revisit
前一段时间借着组里的实习生学习交流的机会,又重新讨论了一次Paxos算法,颇有收获。本文整理记录几个我个人觉得比较有意义的问题,希望通过思考这几个问题,能够加深你对Paxos算法的理解。
本文假定读者已经对Paxos算法有一定了解(包括原理、正确性证明、执行流程),如果你还不了解Paxos,请移步这里。
Paxos算法流程
在思考问题之前,首先重温一下Paxos算法的流程,同时统一变量名称,方便后文讨论。
Prepare阶段:
- Proposer选择proposal number n,并向acceptors发送Prepare(n)消息
- Acceptor收到Prepare(n):if n > minProposal then minProposal = n; return (acceptedProposal, acceptedValue)
Accept阶段:
- 如果Proposer收到了超过多数派acceptors对于Prepare(n)的回复,如果回复中有包含acceptedValue,则选择acceptedProposal值最大的作为value,否则Proposer可以自行选择value
- Proposer向所有acceptors发出Accept(n, value)消息
- Acceptor收到Accept(n, value):if n >= minProposal then acceptedProposal = n; acceptedValue = value,并回复AcceptAck(n)
- Proposer收到来自多数派acceptors的AcceptAck消息,value已达成决议(chosen)
问题
在上述Paxos算法流程的基础上,仔细思考下面几个问题:
- 为了保证算法在容灾(节点故障重启)场景下的正确性,Acceptor上需要持久化哪些信息?
-
如果Acceptor不持久化acceptedProposal,在Prepare阶段的第2步中minProposal代替,有没有问题?
-
Accept阶段,Proposer不用n覆盖acceptedProposal,仍将其发送给Acceptor,Acceptor收到Accept(n, acceptedProposal, value)之后使用消息中的acceptedProposal而不是n来作为acceptedProposal,有没有问题?
-
在5个节点的情况下,如果修改流程为Proposer要收到4个acceptor对Prepare(n)的回应才可以发送Accept消息,要收到2个acceptor对Accept(n, value)的回应才能确认决议,有没有问题?
-
论文中提到Proposer选择proposal number要递增且不重复,这个要求是不是必要的?如果把Prepare阶段第2步中的>改为>=呢?
WARNING: 强烈建议花一些来仔细思考上面的问题,在得出自己的答案之后再继续往下看
C++实现成员函数检查
最近看到一段代码,感觉非常trick,但也非常有意思,写出来记录一下。
背景是这样的,有一个模板函数 copy_assign ,其作用非常简单,就是将第二参数“拷贝”给第一个参数,但是为了对能够进行深拷贝的类型进行深拷贝,希望的行为是这样的:
如果T有成员函数int assign(const T &),则调用dest.assign(src),并以assign函数的返回值作为返回值;
如果T没有成员函数int assign(const T &),则调用dest=src,并返回0。
函数的原型如下:
|
1 2 |
template <typename T> inline int copy_assign(T &dest, const T &src); |
并且为了降低运行时开销,我们希望这一切是在编译期确定的,所以我们需要在编译期就能够确定类型T是否有assign成员函数,并且根据结果指定对应的行为。
并发编程牛刀小试:SeqLock
Sequential lock,简称seq lock,是一种有点特殊的“读写锁”,Linux内核从2.6版本开始引入,是一种非常简单轻量保护共享数据读写的方法。
基本原理
Sequential lock的原理非常简单,其核心就是通过维护一个序号(sequence)来避免读者(Reader)读到错误的数据,而写者(Writer)在加锁和解锁的过程中递增序号,多个写者之间需要借助于额外的互斥锁来保证互斥关系。
具体来讲,序号初始化为0,读者和写者的流程如下:
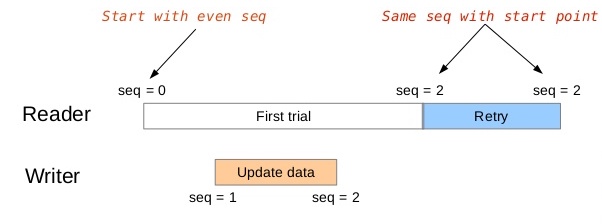
- 写者开始修改临界区中的数据时,首先获取写者间互斥锁,然后递增序号(奇数),开始修改数据,修改数据完成后会再次递增序号(偶数),然后释放写者间互斥锁。
- 对读者来说,在修改数据的过程中读者可能会读到错误的数据,但读者在读数据前后会分别获取一次序号,对两次获取的序号进行比较,如果不相同则说明在读取过程中有写者进入了临界区,需要重试;如果序号相同但是是奇数,说明读者开始读取到结束读取的这段时间写者占有了临界区,同样也需要重试。
看个例子就明白了,如上图所示,是不是非常简洁明了。