相信所有研究过分布式系统的同学都对大名鼎鼎的FLP不可能性有所耳闻,简单来说,FLP不可能性证明了“在可能有哪怕一个进程故障的异步系统模型中,共识问题无法被解决”。但矛盾的是,现在正当红的很多分布式系统,都依赖于底层的共识算法,比如Multi-Paxos、Raft等,难道是FLP错了么?共识问题已经被解决了?还是说我们用的分布式系统都是有问题的?
想要理解这个问题,其实是要搞清楚一件事情:FLP不可能性真正意味着什么?
注:如无特殊说明,本文中的进程故障模型均为crash-stop,通信链路模型为perfect link。
Consensus
首先回顾一下分布式系统中的共识(Consensus)问题是什么。共识问题指在分布式系统中,一个或多个进程提议了一个值应当是什么后,使系统中所有进程对这个值达成一致意见。
一个能够正确的解决共识问题的算法必须满足下面的三个性质:
- 终止性(Liveness):所有正确进程最后都能完成决定。
- 协定性(Safety):所有正确进程决定相同的值。
- 完整性(Integrity):如果正确的进程都提议同一个值,那么所有正确进程最终决定该值。
同步/异步模型
明确了问题,还要看解决问题所用的系统模型是什么样的。
在分布式系统中,最重要的两个系统模型无非就是同步模型和异步模型了。同步模型和异步模型的区别在于对时间的假设,同步模型中消息的传递、进程处理消息所需要的时间都有明确的上界和下界,并且每个进程的本地时间和实际时间的偏移也在一个已知的范围中。而异步模型中没有关于时间的任何假设,是一个没有“时间”概念的模型。
同步模型是理论研究中非常理想的模型,显然的,我们可以在同步模型中用非常简单的方法解决共识问题(各种材料中都会提到,略过),但是在实践中,同步模型是不切实际的,在真实的系统中依靠时间往往是不靠谱的。
这也是为什么我们要研究异步模型的原因:异步模型中的算法是移植性最好的。
在异步模型中正确的算法,在更强的模型中也一定正确,因此,在真实系统中也是正确的。与之相反的是,在同步模型中正确的算法,在更弱的模型中就不一定了,比如3PC算法,在同步模型中解决了2PC的阻塞问题,但是在实践中罕有应用,原因就在这里。
FLP不可能性
在FLP提出之前,有很多研究工作试图在异步模型中解决共识问题,而FLP不可能性的提出,终结了这种尝试。
为了理解FLP不可能性,我们需要主要看一下论文中提出的两个引理:
- Initial Bivalency Lemma (Lemma 2): Any algorithm that solves the 1-crash consensus has an initial bivalent configuration
- Bivalency Preservation Lemma (Lemma 3): Given any bivalent config \(\gamma\) and any event \(e\) applicable, There exists a reachable config \(\delta\) where \(e\) is applicable, and \(e(\delta)\) is bivalent (\(\delta=\gamma\) possible)
简单解释一下引理中涉及的几点定义:FLP论文中把共识问题抽象为所有节点要对一个value最终是0还是1达成共识,config指所有节点的状态和网络中的所有消息;bivalent config指最终共识结果可能为0也可能为1的config;event指的是一个节点收到一条网络消息后执行的动作,只有节点收到网络消息后对应的event才是applicable的。
有了这两条引理再看FLP的证明:我们从bivalent config开始(Lemma 2),反复应用Lemma 3,则整体总是处在bivalent的状态,违背了Liveness的要求。
FLP不可能性提出后,人们不再尝试寻找异步模型中共识问题完全正确的解法,而是对于提出的共识算法,分析其在异步模型中能够解决的部分。
Failure Detectors
从直观上理解,FLP的证明核心在于:在异步模型中,无法准确的区分一个进程究竟是故障了还是运行的非常非常慢。
那么如果我们能够一定程度的判断出进程故障,是不是就可以解决共识问题了呢?在《Unreliable Failure Detectors for Reliable Distributed Systems》这篇论文中就提出在异步模型中通过使用Failure Detector来解决共识问题。
论文首先给出了Failure Detector的两个属性:
Completeness:
- Strong: Eventually every process that crashes is permanently suspected by every correct process.
- Weak: Eventually every process that crashes is permanently suspected by some correct process.
Accuracy:
- Strong: No process is suspected before it crashes.
- Weak: Some correct process is never suspected.
- Eventual strong: There is a time after which correct processes are not suspected by any correct process.
- Eventual weak: There is a time after which some correct process is never suspected by any correct process.
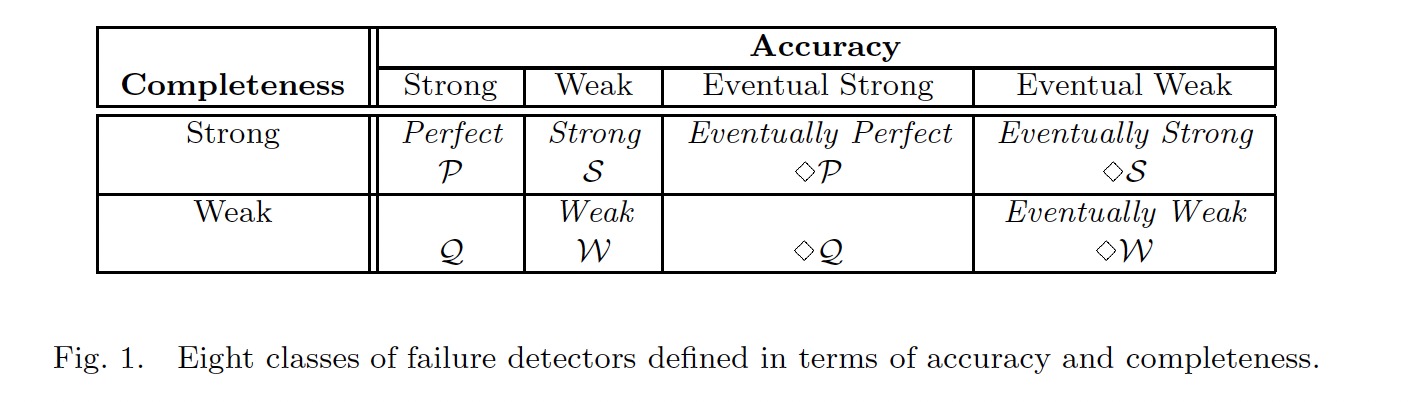
然后按照这两个属性的不同,定义了8类属性不同的Failure Detector:
论文中最为重要的一点的是证明了在异步模型中,Eventuallly Weak Failure Detector是能够解决共识问题所需要的最弱的Failure Detector。
当然,FLP是不可突破的,所以Eventuallly Weak Failure Detector在异步模型中是不可实现的,那你可能要问了,研究这个些个模型还有什么用?毕竟互联网是异步模型啊!实际上,这是一个概率问题,在异步模型中共识达成之前的这段时间里,系统也不一定是那么的“异步”,某种实现的Failure Detector(比如论文中举例的实现方法)有极大概率是可以满足Eventuallly Weak Accuracy的要求的,同理,要依赖更强的Accuracy则意味着更低的成功概率。如果实现的Failure Detector在运行中运气不好没有满足算法需要的Accuracy属性,共识问题不可解,但只会影响到算法的Liveness。
在异步模型中,既然Eventuallly Weak Failure Detector足以解决共识问题,那么还有没有其他问题需要依赖更强属性的Failure Detector才能解呢?答案是有的,比如拜占庭将军问题,就必须要有Perfect Failure Detector的帮助才可以解决。
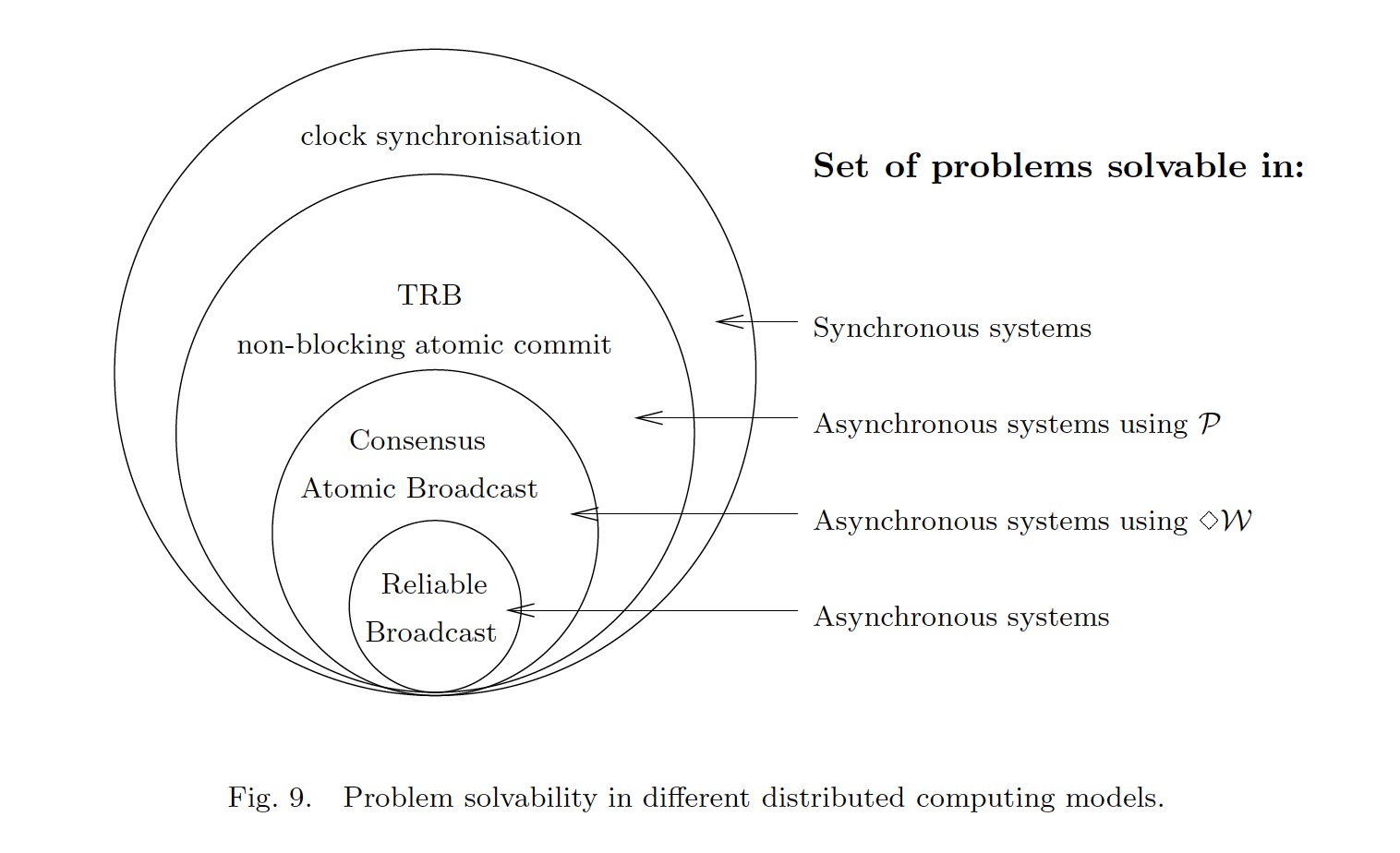
换言之,通过对这些不同强度的Failure Detector的分析,我们能够定义出一些比异步模型更强的模型:
如上图,在异步模型的基础上增加不同的Failure Detector,能够更加准确的定义特定问题可以被解决的模型,填补了同步模型到异步模型之间的灰色地带。除此之外,还有一些其他的研究工作也做了类似的模型定义,例如半同步模型,实际上和这篇论文背后的想法是相通的。
工程实践
现在工程实现中常用的共识算法,都是Paxos及其变种,我们已经知道了FLP算法结论是不可突破的,回顾Paxos算法,在异步模型中,由于活锁的存在,Paxos算法并没有完全解决共识问题(Liveness不满足)。
但是这并不妨碍Paxos算法在各种分布式系统中大行其道,原因就在于上面提到的分析,即使在异步模型中,在达成共识之前,系统并没有那么“异步”,我们仍有极大的概率是可以达成共识的。
这体现了理论研究和工程实践之间的一个“鸿沟”,理论研究中的不可能结论,是在追求100%可解的基础上得出的,在工程实践中,我们可以用一个99.99%的概率可解的算法(剩下的0.01%的场景下由于Liveness不满足,需要更长的时间),也足够好了。
参考资料
[1] Fischer M J, Lynch N A, Paterson M S. Impossibility of distributed consensus with one faulty process[R]. Massachusetts Inst of Tech Cambridge lab for Computer Science, 1982.
[2] Guerraoui R, Schiper A. Consensus: the big misunderstanding [distributed fault tolerant systems][C]//Proceedings of the Sixth IEEE Computer Society Workshop on Future Trends of Distributed Computing Systems. IEEE, 1997: 183-188.
[3] Chandra T D, Toueg S. Unreliable failure detectors for reliable distributed systems[J]. Journal of the ACM (JACM), 1996, 43(2): 225-267.