Coursera上machine learning课程的图标
跟风学习Coursera上Andrew Ng叔的数据挖掘课程已经一个多月了，刚开始在Coursera上看到这门课的时候还有些犹豫，因为研一的时候已经修过学校的数据挖掘课了，那为什么还要再学习这个课程呢？现在想想真是庆幸自己还是选择听听看，原因如下：
- 一年没用数据挖掘，好多知识都忘记了，正好当做复习
- Ng确实很厉害，把看上去非常复杂的理论讲得十分简单清楚，这一定是对问题的本质有很深的理解才能做到的
- lamda的课也是很有水平的，翻翻收藏的ppt，理论功底不可谓不深，但我学艺不精，除去实验外还是不明白在实践中该如何去使用这些工具，Ng的课恰好在这方面是个很好的补充
写到这都和一篇广告软文似的，还是赶紧进入正题吧，趁着脑袋里东西还热乎，赶紧总结一下。PS：本文绝非教程类的文章，而是给自己写的Tips，一则作为学习的记录，二则为以后回忆时方便。如果对这些内容感兴趣，强烈建议直接在Coursera上学习该课程。
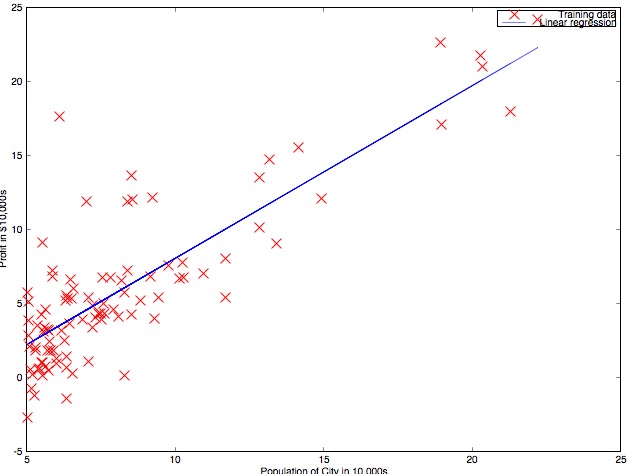
线性回归（Linear regression）
符号表示
- 训练集：\(x\)，其中\(x^{(i)}\)为第\(i\)个训练样本，\(x_j^{(i)}\)代表该样本的第\(j\)个属性；\(y^{(i)}\)表示其对应的正确的回归值
算法概要
Linear Regression
线性回归是一种基本的回归算法，当给出相应的训练集后，通过线性回归来寻找合适参数\(\theta\)（向量）使得Hypothesis函数的Cost function最小：
Cost function所表示的是对应参数\(\theta\)刻画的Hypothesis函数与真实数据的距离，最小化这个距离可以使我们的模型和真实值更加接近。同时，通过增加高次项特征，我们可以使模型更加复杂。
Polynomial regression
梯度下降（Gradient descent)
有很多方法可以实现最小化Cost function，梯度下降是其中最为简单直接的一种。
\begin{aligned}
&Repeat\ \{\\
&\qquad\theta_j=\theta_j-\alpha\frac{\partial}{\partial\theta_j}J(\theta)\\
&\qquad(simultaneously\ update\ for\ every\ j=0,\ldots,n)\\
&\}
\end{aligned}
\)
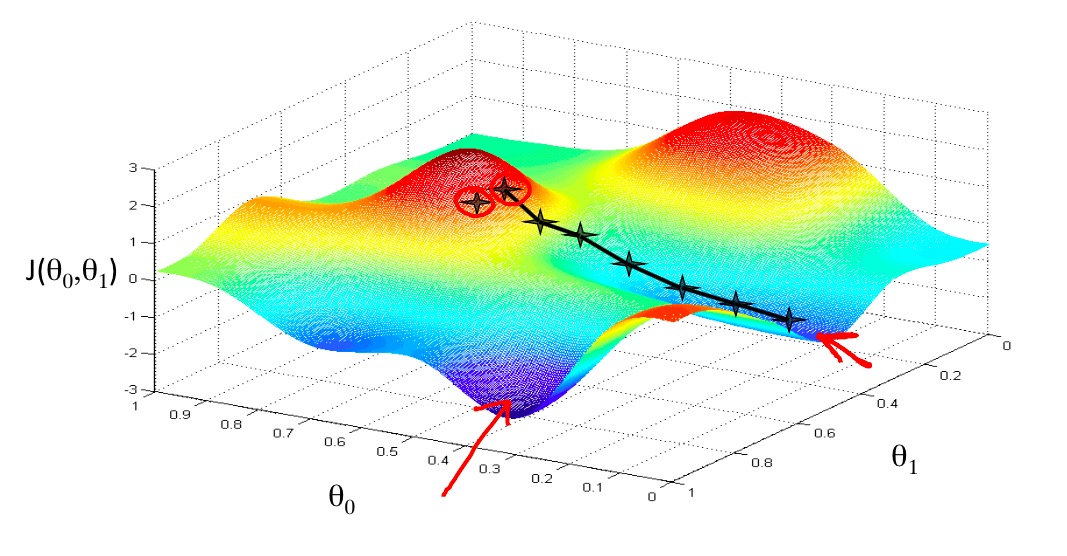
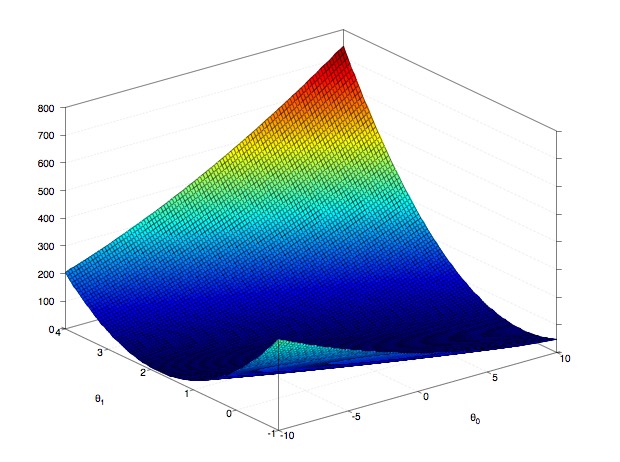
可以看到，梯度下降的思想非常的简单：每次迭代中向梯度最大的方向按照learning rate\(\alpha\)下降，直到到达整个函数的局部/全局最优点，Ng的slides中的示意图很好的表示了这个思想：
Gradient descent
通过不断的调整参数，使其不断的朝着Cost function下降的方向改变，最终达到一个最小点。在线性回归中，由于Cost function没有局部最优解，所以梯度下降一定会得到全局最优解。
Gradient descent in linear regression
梯度下降并不是唯一的降低Cost function的方法，还有更多更加高级的解法可以达到相同的效果，在之后的project中Ng更多的使用fminunc而非梯度下降来获得更好的实现效率。
特征缩放（Feature scaling）
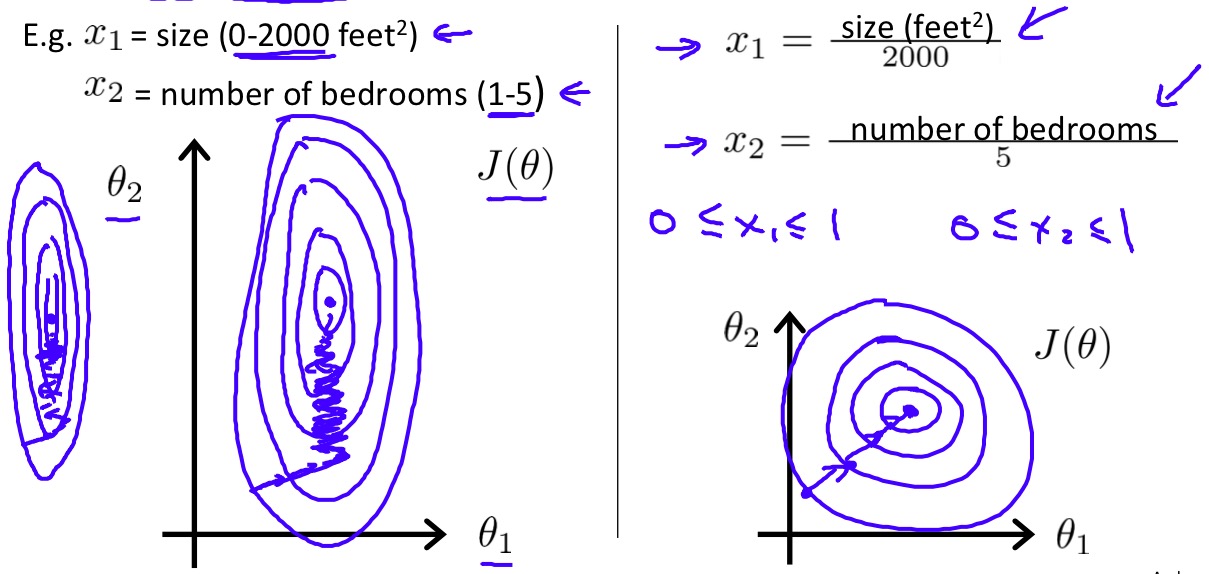
当多个特征的取值范围不同并且相差很大时，会给梯度下降带来不小的麻烦，梯度下降过程会变得非常的缓慢，因此在多个特征取值范围相差较大时，我们首先应该对这些特征进行缩放以确保他们具有相同的取值范围。
Feature scaling
逻辑回归（Logistic regression）
在线性回归的基础上解释逻辑回归非常的简单。逻辑回归和名字所暗示的不同，逻辑回归是一个分类算法！首先讨论二分类的情况，即判断样本\(x\)是否属于正类型。
逻辑回归的Hypothesis和线性回归非常相似
\begin{aligned}
h_\theta(x)=&g(\theta^{T}x)\\
g(z)=&\frac{1}{1+e^{-z}}
\end{aligned}
\)
唯一的区别在于外层的sigmoid function，详情戳这里。
Sigmoid function
简单来说，当参数大于0时，则函数值趋近于1，而当参数值小于0时，函数值趋近于0。因此逻辑回归的Hypothesis可以解释为样本\(x\)属于正类型的概率。当\(\theta^{T}x>0\)后，概率趋近于1，反之则趋近于0。由此得到Cost function如下：
Cost function看上去复杂，实际上如果仔细分析，其实函数表示的意义非常简单：当预测的概率越接近真实情况，代价函数越接近0，反之则趋近于无穷大。
之后可以和线性回归一样，采用梯度下降或其他方法来寻找合适的参数\(\theta\)使Cost function最小化，得到训练后的模型。
Logistic regression
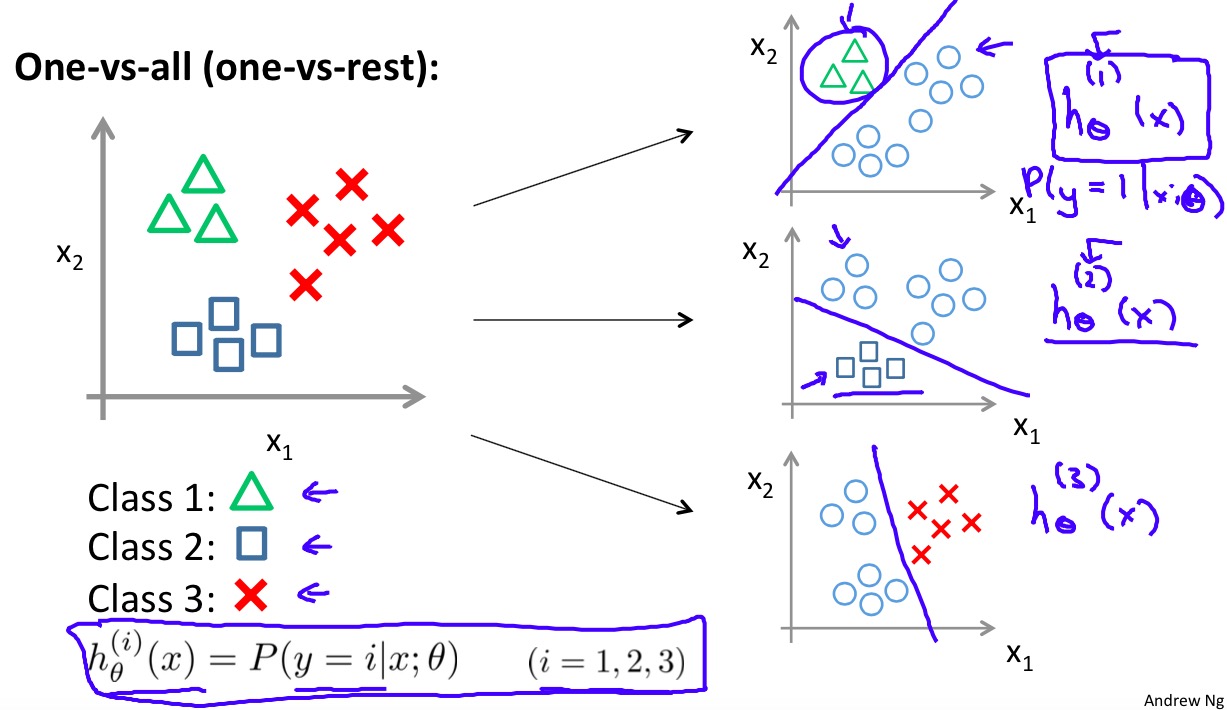
One-vs-all
在二分类的基础上，通过one-vs-all的方法得到多类别的分类器。one-vs-all的基本思想是为每一个类\(i\)都训练一个二分类分类器\(h_\theta^{(i)}(x)\)，当分类预测时选择概率最大的类别作为结果。
One-vs-all
Bias、Variance以及Regularization
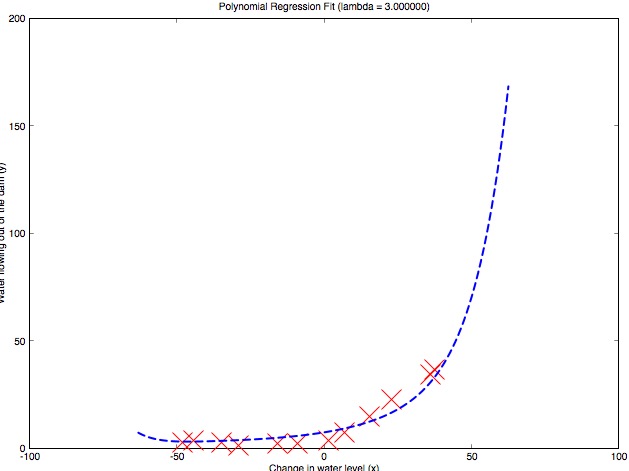
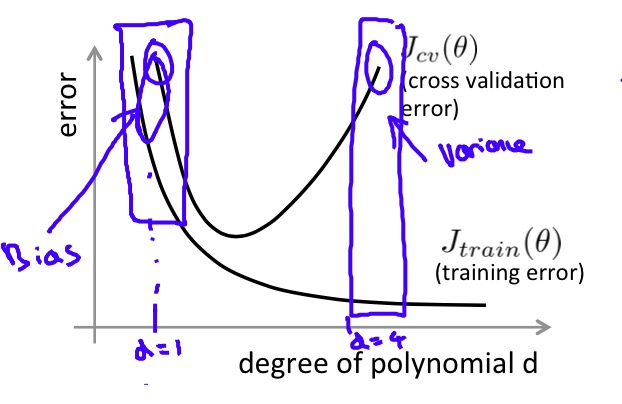
接下来需要讨论一个前面一直避而不谈的问题：Bias和Variance。这两个词意思都不是很直白，简单来说，high Bias的含义就是模型太过于简单，不能很好对训练集进行学习，属于under-fitting；而high Variance则相反，代表了模型太过于复杂，甚至拟合了训练集中的噪声，属于over-fitting，虽然training error很低但是泛化误差大，会有很高的test error。
Bias vs Variance
如上图所示，当模型非常简单时，训练误差和验证误差都很大，说明模型under-fitting（high Bias），随着模型越来越复杂（次数越来越高），对训练集的学习越来越到位，训练误差和验证误差都逐渐减小，然而在超过某一程度后，模型过于复杂，出现了over-fitting（high Variance），验证误差开始增大。
Regularization正是为了让我们在模型的复杂性和泛化能力之间做出一个平衡。通过在Cost function后增加一个Regularization项来避免训练出过于复杂的模型，线性回归Regularization之后的Cost function如下：
J(\theta)=\frac{1}{2m}\left[\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum_{j=1}^{n}\theta_j^2\right]
\)
逻辑回归Regularization之后的Cost function如下：
\begin{aligned}
J(\theta)=&-\frac{1}{m}\left[\sum_{i=1}^{m}y^{(i)}\log h_\theta(x^{(i)})+(1-y^{(i)})\log (1-h_\theta(x^{(i)}))\right]\\
&+\frac{\lambda}{2m}\sum_{j=1}^{n}\theta_j^2
\end{aligned}
\)
Regularization parameter的作用相当于对每一个参数增加了惩罚，以避免模型变得过于复杂，另外注意对常数参数\(\theta_0\)不做Regularization。
总的来说，Ng所建议的数据挖掘实践是首先写出一个最为简单粗糙的模型，然后根据模型的learning curve，观察模型处于high Bias还是high Variance状态，然后做出对模型进行改进的决策，如果模型处于high Bias，我们可以：
- 增加更多特征
- 减小\(\lambda\)
而如果模型处于high Variance中，我们可以：
- 收集更多的训练数据集
- 减少特征
- 增大\(\lambda\)
神经网络（Neural network）
终于写到了神经网络，窃以为Ng之所以要讲线性回归和逻辑回归完全是为了讲他最爱的神经网络…如Ng所说，神经网络是现在“most powerful”的学习算法，可以学习非常非常复杂的模型。
神经元
Neuron model
每次学习神经网络总是在第一步看到神经元的地方就愣住了，“这是啥…为啥要这么做…这能训练出啥…”，当在Ng课上再次看到这个神经元模型，终于恍然大悟，这货不就是个逻辑回归么！！！输入为\(x\)，神经元的输入边权构成参数\(\theta\)，激活函数sigmoid函数…和逻辑回归的Hypothesis一样样的…
\begin{aligned}
h_\theta(x)=&g(\theta^{T}x)\\
g(z)=&\frac{1}{1+e^{-z}}
\end{aligned}
\)
神经网络
Neural network
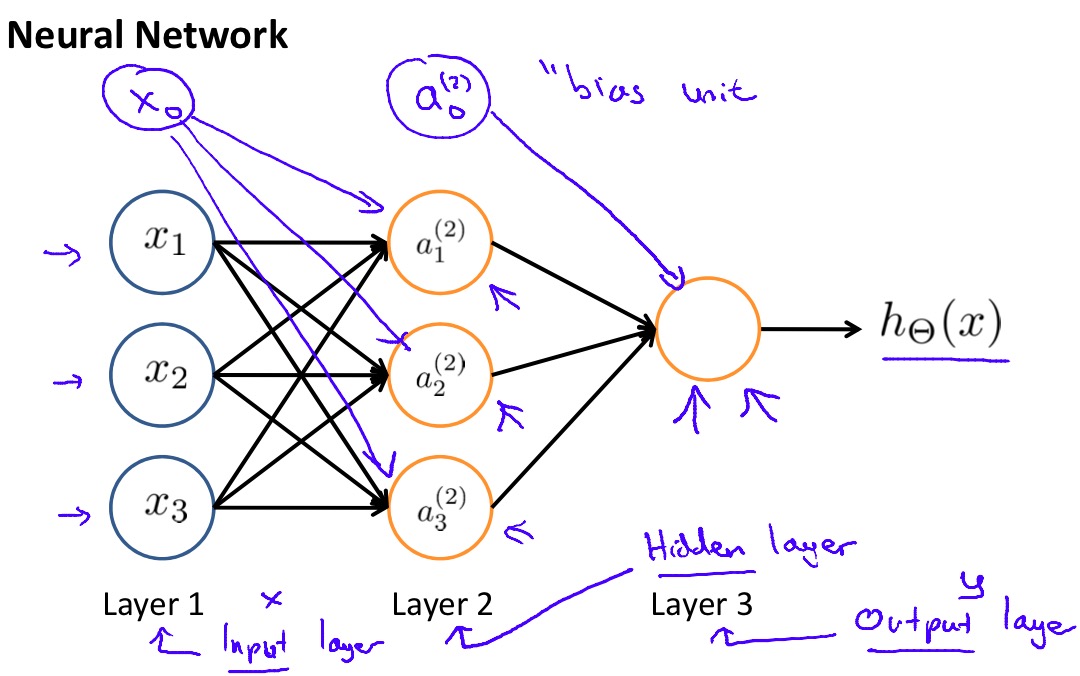
于是神经网络似乎也就不是那么难以理解了，神经网络的第一层是输入层，值为\(x_i\)，最后一层是输出层，如果作为分类算法训练则有多少个类别就应该有多少个对应的输出单元，对应的输出单元被激活代表着分类的结果。有意思的事情发生在中间的隐藏层，隐藏层可以有多层，每层可以有多个单元，规模越大训练的模型越复杂。而对于隐藏层中的每个单元本身都是一个逻辑回归的过程，也就是说每个隐藏单元都训练出了一个比前一层更加复杂的特征，这样一层接一层我们就可以训练出越来越复杂的特征，直到得到结果。
前向传播
在已经训练好权值的神经网络上，预测的工作是通过前向传播来实现的，所谓的“前向”就是从输入层到输出层的方向。整个传播过程就是沿着神经网络的方向在每个神经元上做逻辑回归，不断训练出更加复杂的特征，最后得到输出。以上图的神经网络为例：
\begin{aligned}
z^{(2)}=&\Theta^{(1)}a^{(1)}\\
a^{(2)}=&g(z^{(2)})\\
Add\ a_0^{(2)}=&1\\
z^{(3)}=&\Theta^{(2)}a^{(2)}\\
h_\Theta(x)=&a^{(3)}=g(z^{(3)})
\end{aligned}
\)
其中\(z^{(i)}\)表示第\(i\)层神经元的输入，\(a^{(i)}\)表示第\(i\)层神经元的输出，\(\Theta^{(i)}\)表示第\(i\)层神经元输入边的权值。
后向传播
虽然神经网络比逻辑回归要复杂的多，但训练的基本思路还是相同的，即修改参数\(\Theta\)来获得最小的Cost function。那么首先来看看神经网络的Cost function:
\begin{aligned}
J(\Theta)=&-\frac{1}{m}\left[\sum_{i=1}^{m}\sum_{k=1}^{K}y_k^{(i)}\log (h_\Theta(x^{(i)}))_k+(1-y_k^{(i)})\log (1-(h_\Theta(x^{(i)}))_k)\right]\\
&+\frac{\lambda}{2m}\sum_{l=1}^{L-1}\sum_{i=1}^{s_l}\sum_{j=1}^{s_{l+1}}(\Theta_{ji}^{(l)})^2
\end{aligned}
\)
看上去是不是复杂到爆表…别着急，对应逻辑回归的Cost function，神经网络的版本只是把\(K\)个类的代价加起来了而已，后面的Regularization项也只是针对神经网络的特点对\(\Theta\)中每一项进行了惩罚。
那么接下来该如何最小化Cost function呢？还是梯度下降的老办法，不过在神经网络的训练中\(\frac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta)\)就不像前面两种算法中那么容易求了。后向传播就是为了解决这个问题而提出的。后向传播的基本思想是对每一个训练样本，根据这个样本的预测结果误差从后向前的计算出这次预测中每个神经元的误差，\(\delta_j^{(l)}\)表示第\(l\)层上\(j\)神经元的误差，还是以上图中神经网络为例，我们可以后向求出整个神经网络中所有神经元的误差：
\begin{aligned}
\delta^{(4)}=&a^{(4)}-y\\
\delta^{(3)}=&(\Theta^{(3)})^{T}\delta^{(4)}.*g'(z^{(3)})\\
\delta^{(2)}=&(\Theta^{(2)})^{T}\delta^{(3)}.*g'(z^{(2)})
\end{aligned}
\)
整体的后向传播算法就是对每一个训练样本执行上面的过程，并不断积累\(a_j^{(l)}\delta_i^{(l+1)}\)（略过复杂的数学证明）如下：
Backpropagation
最后的等式\(\frac{\partial}{\partial{\Theta_{ij}^{(l)}}}J(\Theta)=D_{ij}^{(l)}\)涉及到复杂的数学证明，Ng也没有详细解释。总之通过一通计算我们得到了想要的\(\frac{\partial}{\partial\Theta_{ij}^{(l)}}J(\Theta)\)，然后使用梯度下降或是更高级的算法来对Cost function进行最小化，这里特别注意虽然神经网络中Cost function并不是convex函数，即存在局部最优解，但Ng说这不碍事，通常即使是局部最优解也会得到相当不错的效果。
PS.后向传播算法的原理相当复杂，我是没能力讲清楚了…请参见Ng的课程吧。
随机初始化
在神经网络中训练初始化时，要特别注意不能使\(\Theta\)中的值都相同，这样会使每一层的神经元都训练出完全相同的特征，神经网络就完全无法工作了。因此，在训练开始前，应该对\(\Theta\)进行随机的初始化。
举个栗子
Ng课程的编程作业中给出了一个蛮好玩的例子：识别手写数字。
numbers
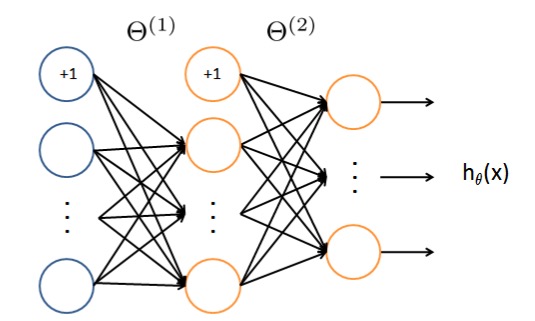
数字识别过程首先将20*20的数字图片转换为400维的灰度向量输入神经网络，使用下面结构的神经网络进行训练，输入层有401个节点（包括1个Bias节点），隐藏层包含25个神经元，输出层有10个神经元对应10个数字类别，最终获得了非常赞的效果~
Neural network model
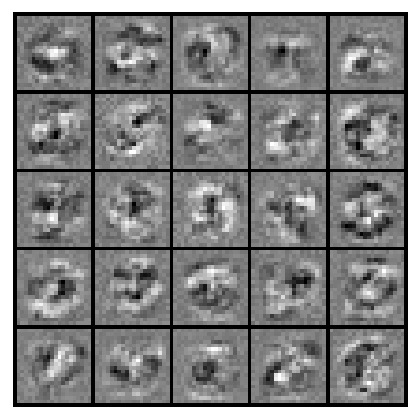
下图对训练好的隐藏层25个神经元参数进行了可视化，可以看到每个神经元都训练出了一个更加复杂的特征，神经网络就是通过不断训练出这些比原始灰度特征更加复杂的特征才能得到如此优秀的效果。
Hidden layer
参考资料
- Machine Learning by Andrew Ng on Coursera
啰嗦两句
感谢Coursera，感谢MOOC让我们能享受到这么高质量的课程。我要努力成为一个终身学习者！！！
感谢院士提供\(\LaTeX\)语法支持。