斯坦福在coursera上的博弈论课程又开放了,这么高大上的课程怎么能错过呢?现在课程已经过半,回过头来对前几周的内容做个小结。
什么是Game?
博弈论中的game不是指我们平时玩的电脑游戏,而是指代多个角色之间进行的“博弈”,比如说非常流行的“石头-剪子-布”的游戏。
具体来讲,game由以下几个部分组成:
- Players:参与博弈的主体
- Actions:Player可以采取的行动
- Payoffs:Player行动可以获取的回报
博弈论中对所谓game有不同的描述形式:Normal form game用来表示一些Payoffs可以看做是Actions的函数的game,在这种game中Players往往同时采取行动(或可以看做是同时),而Extensive form game中引入了时间的概念,Players按次序采取行动,如扑克,象棋等。
这次我们先关注Normal form game,形式化定义一个可终止(Finite)的\(n\)主体的game为:\(\langle N, A, u\rangle\):
- Players:\(N= \left\{ 1,\dots,n \right\} \)表示参与博弈的主体,以\(i\)作为索引
- Actions:\(A_i\)表示Player \(i\)可以采取的Actions集合,定义action profile为\(a=(a_1,\dots,a_n)\in A=A_1\times \dots \times A_n\),表示一组可能出现的情况
- Payoffs:\(u_i\)表示Player \(i\)的utility function,用来计算特定action profile下Player \(i\)可以获取的回报:\(u_i(a), a\in A\)
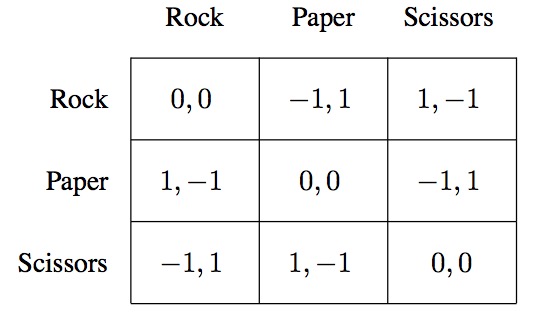
举个栗子,将“石头-剪子-布”游戏展现为Matrix如下:
游戏中\(N=\{1,2\}\),\(A_1=A_2=\{Rock, Paper, Scissors\}\),对应的Payoffs写在表格中,当\(a=\{Paper, Paper\}\)时,\(u_1(a)=u_2(a)=0\),表示平局。
Strategy
除了Actions,game中还有一个重要的概念:Strategy。Strategy表示了Player如何使用Actions的“策略”,形式上来讲,对Player \(i\)有strategy \(s_i\),代表Actions集合\(A_i\)上的一个概率分布。
大体上可以将所有strategy分为两种:
- pure strategy:是一种特殊情况,在集合\(A_i\)中仅有一项概率为正(为1?),这种情况下该strategy即确定了使用某一Action
- mixed strategy:混合策略引入了随机性,strategy按一定概率使用不同的Actions
对于Player \(i\),\(S_i\)表示其所有可用的strategy的集合,和Actions类似定义strategy profile \(s=(s_1,\dots ,s_n)\in S=S_1\times \dots \times S_n\),表示一组在游戏中各个Player使用的strategy。
因为有了strategy的概念,我们需要一个新的能够针对给定strategy profile计算回报的utility function,由于不是单一Action,我们需要将头脑切换至概率模式研究下面的公式:
\begin{aligned}
u_i(s)=&\sum_{a \in A}u_i(a)Pr(a|s)\\
Pr(a|s)=&\prod_{j \in N}s_j(a_j)
\end{aligned}
\)
看上去很复杂,实际上可以按照概率论中期望值的感觉来理解:如果用这样的strategy profile进行大量试验,某个Player期望获得的Payoff是多少?
Best response
既然是game,那么每个Player都希望自己可以赢(获得尽可能高的Payoff),由此引出了best response的概念。
在pure strategy中,假如Player \(i\)已经知道了其他Players的行动\(a_{-i}=\langle a_1,\dots,a_{i-1},a_{i+1},\dots,a_n \rangle\),那么他可以根据情况做出best response \(BR(a_{-i})\),定义如下:
\[
a_i^* \in BR(a_{-i}) \iff \forall a_i \in A_i,u_i(a_i^*,a_{-i}) \geq u_i(a_i,a_{-i})
\]
在mixed strategy中,同样类似的如果Player \(i\)已经知道了其他Players的strategy \(s_{-i}=\langle s_1,\dots,s_{i-1},s_{i+1},\dots,s_n \rangle\),那么他可以根据情况做出best response \(BR(s_{-i})\),定义如下:
\[
s_i^* \in BR(s_{-i}) \iff \forall s_i \in S_i,u_i(s_i^*,s_{-i}) \geq u_i(s_i,s_{-i})
\]
Nash equilibrium
然而在实际的博弈过程中,任何一个Player实际上并不知道他的对手们会采用什么样的action \(a_{-i}\)(或者strategy \(s_{-i}\)),但是经过实践验证,在这样的博弈过程中Players为了争取最大化Payoffs,Players之间相互的制约关系导致他们所做的选择会逐渐趋向于形成“稳定”的action profile(或stategy profile),这样的profiles就是Nash equilibrium。
Nash equilibrium具有的特征是:所有Player采用的action(或者strategy)都是best response。这意味着任何Player都没有办法采用其他的方法来获得更好的Payoff了。
形式化来讲,对于pure strategy:
\[
a=\langle a_1,\dots,a_n\rangle\ \text{is a (“pure strategy”) Nash equilibrium} \iff \forall i,a_i\in BR(a_{-i}).
\]
对于mixed strategy:
\[
s=\langle s_1,\dots,s_n\rangle\ \text{is a (“mixed strategy”) Nash equilibrium} \iff \forall i,s_i\in BR(s_{-i}).
\]
Nash在1950年证明了所有有穷的(finite)的game都存在Nash equilibrium。但要注意,这个证明针对于mixed strategy nash equilibrium,并不一定存在pure strategy nash equilibrium。
这有什么用呢?研究Nash equilibrium意味着如果我们知道了一个game的基本元素:Players、Actions、Payoffs,则我们可以通过寻找这个game的Nash equilibrium来对Players的行为做出一些预测和判断。
点球博弈
来看一个非常有意思的例子:罚点球。
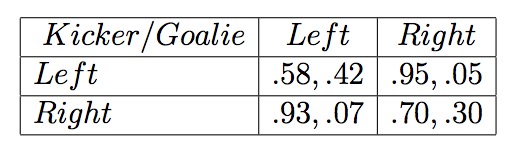
Ignacio Palacios-Heurta在2003年的论文“Professionals Play Minimax”中对1417场西班牙、英国、意大利的FIFA联赛中出现的点球进行了统计,得出下面的game:
参与博弈的双方毫无意外的是射手(Kicker)和守门员(Goalie),双方的Actions均包含两个方向:向左踢(扑救)或者向右踢(扑救),Payoffs可以看做是射进点球的概率和成功守住的概率。
很明显可以看出在这个game中不存在pure strategy nash equilibrium(双方总可以通过选择相反方向获得更高的回报),那么我们来寻找它的mixed strategy nash equilibrium。
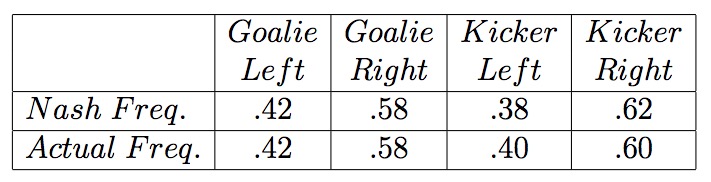
下图是我们所求得的mixed strategy nash equilibrium,可以看到和真实统计得到的结果非常接近!
虽然球场上双方球员都没有经过这样一系列运算,但是最终的结果居然惊人的一致!是不是很神奇~
参考资料
- 《Game Theory Course: Jackson, Leyton-Brown & Shoham》on Coursera