继续上次的笔记,记录下之前几周课程中我觉得比较有意思的一个问题:大名鼎鼎的囚徒困境(Prisoner’s dilemma)。
囚徒困境
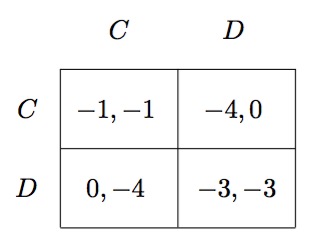
囚徒困境实在是太经典了,一个通俗的例子是说一件案子的两个罪犯(团伙)同时被逮捕并且带到警察局分别审问,两个罪犯之间无法沟通,每个罪犯都可以选择抵赖(Collaborate 即与对方合作)或是交代(Defect 即背叛对方),可能的结果如下:
- 如果两个罪犯同时选择抵赖,由于证据不足,只能判两个罪犯都服刑一年
- 如果其中一个罪犯选择抵赖而另一个罪犯选择交代,则选择的抵赖的罪犯被判服刑四年,而选择交代的罪犯被赦免,无需服刑
- 如果两个罪犯同时选择交代,则两个罪犯都要服刑三年
展现为Matrix如下:
从全局的观点来看,两个罪犯应该选择合作(即全部抵赖),这样两个罪犯都服刑一年,是一个较优的全局解,但是由于两个罪犯不能确定对方会选择什么,从单个罪犯的角度来想,都会担心对方为了他个人的利益而出卖自己,凸显了人性本恶,囧…
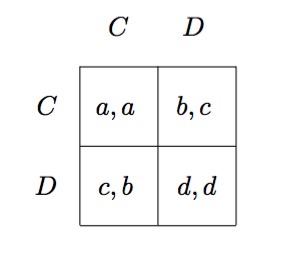
囚徒困境实际上是一类game,其Matrix如下:
只要这个game中满足\(c>a>d>b\),就是一个囚徒困境问题。
走出困境
假如你是其中一个罪犯,你会如何选择?没错,我当然要best response对方的Action,于是乎,Nash equilibrium出现了!当两个罪犯都选择\(D\),即背叛对方的时候,任何一方都没有办法获得更好的Payoff了。
吐个槽:这个解明显是警察更愿意看到的,所以才有了美剧中各种隔离审问,“他已经出卖了你”、“我们来做个交易”等等之类的桥段么…
悖论(The paradox)?
但是,这样的局面看上去似乎很奇怪?为什么双方最后会选择出一个从团体角度来看直观上最差的outcome呢?
本质上来讲,因为这样的game中,Players都是self-interested Agent,即Player没有全局观,他们选择的Action都是基于自己所能获得的Payoff,而非整体的Payoff。
从全局的角度来看问题,Players之间并没有优劣之分,那么又该如何判断哪一个outcome是更好的呢?
由此引出Pareto Optimality的概念:
- 假设一个outcome \(o\)对于任何一个Player所能获得的Payoff都不差于在另一个outcome \(o’\)中获得的Payoff,则称\(o \text{ Pareto-dominates } o’\)
- 当存在一个outcome \(o^*\),没有任何一个其他的outcome可以Pareto-dominates它,则称其为Pareto-optimal
例如在先前所举的囚徒困境中,action profile \((C,C),(C,D),(D,C)\)所对应的outcome都是Pareto-optimal,而Nash equilibrium \((D,D)\)所对应的outcome是唯一一个non-Pareto-optimal的outcome!
也就是说,这样的博弈中Nash equilibrium总会得到团体收益最低的outcome,这也是『悖论』所在:非零和博弈中,Pareto-optimal和Nash equilibrium是互相冲突的。
重复囚徒困境
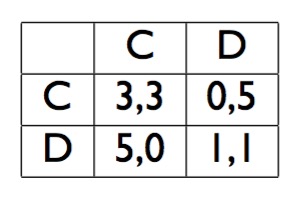
然而,当我们重复进行囚徒困境时,情况产生了变化。
试想一下在上图所描述的stage game中,如果我们随着时间推移不断的进行这样的game(无穷次),双方都不能仅仅只考虑眼前的利益,还需要考虑长远的收益:选择背叛虽然可以获取较大的短期回报,但是对方可以选择在之后的game中进行报复,导致长期回报遭受损失。
比如在重复囚徒困境中就有两个非常有名的策略:
- tit-for-tat:以牙还牙,刚开始选择合作,一旦对方背叛,则下一回合选择背叛惩罚对方,然后回到合作状态
- triger:触发,刚开始选择合作,一旦对方背叛,则之后永远选择背叛惩罚对方
在无限重复博弈中,衡量收益的Utility函数必然也会发生变化,一种建模方式认为Player相对未来的Payoff来讲更重视当前对局的Payoff,假定Player \(i\)对未来Payoff的重视因子为\(\beta\),且\(0<\beta<1\),Player \(i\)所获得的Payoffs序列为Player \(r_1,r_2,\dots\),那么Player \(i\)所获得的的整体收益为:
\[\sum_{j=1}^\infty \beta^jr_j\]
假如你是这里的Player之一,且你知道你的对手采用triger策略,那么该怎么判断要不要背叛对方么?
当然是在背叛的利益超过合作的利益的时候!(人性啊…)
与对方持续保持合作的收益为:
\[3+\beta 3+\beta ^2+\beta ^33\dots=\frac{3}{1-\beta}\]
背叛对方后被惩罚的总收益为:
\[5+\beta 1+\beta ^21+\beta ^31\dots=5+\beta\frac{1}{1-\beta}\]
两者之差为:
\[-2+\beta 2+\beta ^22+\beta ^32\dots=\beta\frac{2}{1-\beta}-2\]
当\(\beta > 1/2\)时,有两者之差大于0,此时与对方保持合作才是上策。
换个角度来看,我们越重视未来的收益,就越倾向于与对方合作;另一方面,背叛所带来的利益越高,也就越有可能导致一方的背叛,和直觉非常相符。
参考资料
- 《Game Theory Course: Jackson, Leyton-Brown & Shoham》on Coursera