有向图强连通分支算是个基础算法,不过总是忘记,写下来备忘。
无向图强连通分支非常简单,使用图的遍历算法(DFS或BFS)即可,而有向图的强连通分支计算则要复杂一些,Kosaraju’s algorithm实现了\(O(n+m)\)时间复杂度的有向图强连通分支算法。
算法的核心思想在于:从有向图中任何一个点出发做DFS,必然能从图中“拖”出一个点集,和无向图中不同的是,这个点集不一定构成强连通分支,但是如果我们能通过一个合适的顺序进行DFS(“sink” vertex),则可以依次把每一个强连通分支“拖”出来,得到正确的结果,那么算法的要点则在于如何寻找这个合适的顺序。
算法通过两次DFS来求解,步骤如下:
- 对原图\(G\)做反转(reverse)操作,即将所有有向边逆置,得到图\(G^{rev}\)
- 在图\(G^{rev}\)上做后序的DFS,得到点遍历顺序
- 按照上一步中得到的遍历顺序,从大到小在原图\(G\)中通过DFS依次“拖”出强连通分支
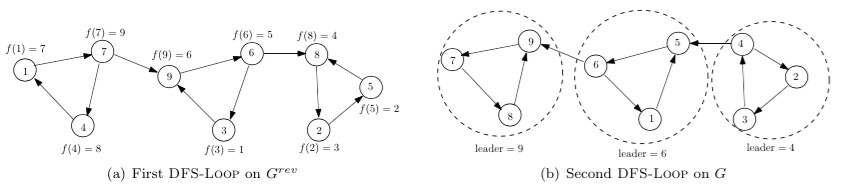
运行过程如下图例,\(f(v)\)代表点在\(G^{rev}\)的遍历结束时间,从9号点开始DFS。
记得刚学习这个算法时一直有的一个疑惑:为什么在第一遍DFS时一定要在图\(G^{rev}\)上做么?难道不能通过在原图\(G\)上DFS的顺序从小到大的进行第二次DFS么?仔细研究算法正确性的证明,不难发现这个想法是错误的。
该算法正确性证明的核心在于对于图\(G\)中任意两个相邻的强连通分支\(C_1\)和\(C_2\)且存在边\((i,j)\)满足\(i \in C_1 \land j \in C_2\)(在强连通分支的DAG中方向为\(C_1 \to C_2\)),可以证明:
\(f(v)\)代表点在\(G^{rev}\)的遍历结束时间,因此,在图G中具有最大\(f(v)\)的点一定为“sink” vertex。
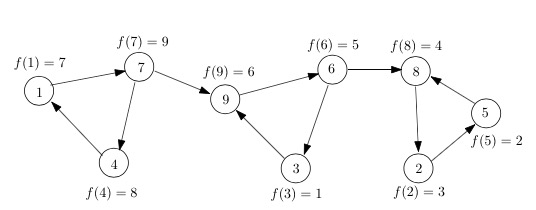
那么现在来看看之前的想法错在哪里了,令\(f'(v)\)代表点在\(G\)的遍历结束时间,如果按照从小到大的顺序在\(G\)可以依次“拖”出强连通分支,则我们需要证明(强连通分支\(C_1\)和\(C_2\)的定义同上):
显然这是不对的…反例见下图中强连通分支{9,6,3}和{8,5,2},\(f'(3)=1\)比{8,5,2}中的完成时间都要小,如果从该点开始“拖”强连通分支得到的是错误的结果{9,6,3,8,5,2}。
所以\(G^{rev}\)的计算是必不可少的。
代码如下,采用递归实现DFS,在实际使用中容易造成栈溢出,修改为非递归实现即可。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 |
#include <vector> #include <list> #include <stack> #include <iostream> #include <fstream> #include <cassert> #include <unordered_map> #include <algorithm> using namespace std; class Graph { public: Graph(int n) { _storage.resize(n); } void addVertex() { _storage.push_back(list<int>()); } void addEdge(int vertex, int adjacent) { _storage[vertex].push_back(adjacent); } int vertices() { return _storage.size(); } int edges() { int count = 0; for (int i = 0; i < vertices(); ++i) { count += _storage[i].size(); } return count; } list<int> &edges_for_vertex(int vertex) { return _storage[vertex]; } private: vector<list<int> > _storage; }; class SCC { public: vector<int> calculateSCC(Graph &g) { int n = g.vertices(); Graph g_rev(n); for (int v = 0; v < n; ++v) { list<int> &edges = g.edges_for_vertex(v); for (int u : edges) { g_rev.addEdge(u, v); } } assert(g.edges() == g_rev.edges()); stack<int> s; vector<bool> map(n, false); // first pass for (int i = 0; i < n; ++i) { if (!map[i]) { dfs_order(g_rev, i, s, map); } } vector<int> ssc(n, -1); // second pass while (!s.empty()) { int i = s.top(); s.pop(); if (ssc[i] < 0) { dfs_ssc(g, i, i, ssc); } } return ssc; } private: void dfs_order(Graph &g, int v, stack<int> &s, vector<bool> &map) { map[v] = true; list<int> &edges = g.edges_for_vertex(v); for (int u : edges) { if (!map[u]) { dfs_order(g, u, s, map); } } s.push(v); } void dfs_ssc(Graph &g, int v, int leader, vector<int> &ssc) { ssc[v] = leader; list<int> &edges = g.edges_for_vertex(v); for (int u : edges) { if (ssc[u] < 0) { dfs_ssc(g, u, leader, ssc); } } } }; vector<int> rankSCC(vector<int> &scc) { unordered_map<int, int> count; for (int i = 0; i < scc.size(); ++i) { if (count.find(scc[i]) != count.end()) { count[scc[i]] += 1; } else { count[scc[i]] = 1; } } vector<int> rank; for (auto it = count.begin(); it != count.end(); ++it) { rank.push_back(it->second); } sort(rank.begin(), rank.end()); return rank; } int main(int argc, char *argv[]) { ifstream fin("SCC.txt"); int n = 875714; Graph graph(n); while (fin) { int s = 0, t = 0; fin >> s >> t; if (s != 0 && t != 0) { graph.addEdge(s - 1, t - 1); } } cout << graph.edges() << " lines loaded." << endl; SCC solver; vector<int> scc = solver.calculateSCC(graph); vector<int> rank = rankSCC(scc); int total = 0; for (int i = 0; i < rank.size(); ++i) { total += rank[i]; } assert(total == n); for (int i = rank.size() - 1; i >= rank.size() - 5; --i) { cout << rank[i] << ','; } cout << endl; return 0; } |
好吧,我承认我就是为了凑数的…
参考资料
- Algorithms: Design and Analysis, Part 1 by Tim Roughgarden on Coursera