写这篇小结的时候，Ng的课程已经结束了（期待SoA哈哈哈），回顾整个课程内容，虽然Ng有意的屏蔽了大部分的数学内容，但是提纲挈领的为我们展现了常见机器学习算法的基本容貌和应用技巧，令人受益良多。从视频、课后问答到编程作业，都完美的示范了一门在线课程应该是什么样子的，不能感谢更多。

回到正题，异常检测，也称为离群点检测，是用来发现一些特征不同于预期的样本，在应用中具有极高的价值。异常检测有多种方法，Ng课程中讲的是基于统计学方法（高斯模型）的异常检测。

---

异常检测

首先复习一下高斯分布（正态分布）：

对于均值为\(\mu\)方差为\(\sigma^{2}\)的随机变量\(X\)，若其服从正态分布，称\(X\sim N(\mu,\sigma^{2})\)，概率密度函数为：

\(\displaystyle
p(x;\mu,\sigma)=\frac{1}{\sigma \sqrt{2\pi}}\exp\left(-\frac{(x-\mu)^{2}}{2\sigma^{2}}\right)
\)

基于高斯模型的异常检测idea非常的简单：假设样本特征服从高斯分布（分单变量和多变量两种），通过训练集（正常样本）拟合出高斯分布的参数\(\mu,\sigma^{2}\)，然后对于预测样本计算出该分布中的概率密度，如果概率小于\(\epsilon\)则认为是异常样本。

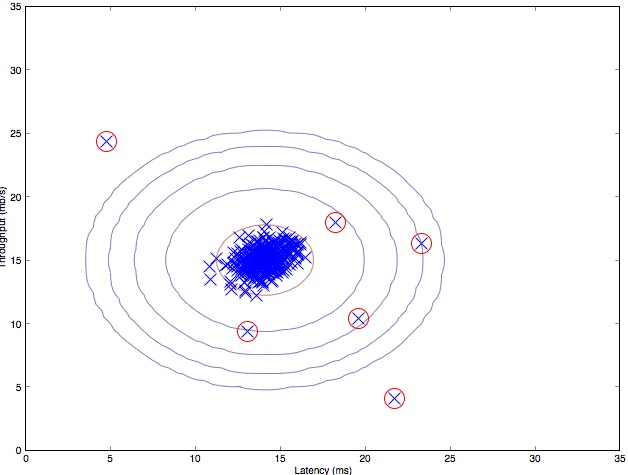
下图是对两个特征的样本进行异常检测的结果，红色圈出的是检测出的异常样本：

单变量高斯分布

使用单变量高斯模型的异常检测中，我们认为样本的每个特征都服从独立的高斯分布，为这些特征单独拟合参数：

\(\displaystyle
\mu_j=\frac{1}{m}\sum_{i=1}^{m}x_j^{(i)} \\ \displaystyle
\sigma_j^2=\frac{1}{m}\sum_{i=1}^{m}(x_j^{(i)}-\mu_j)^2
\)

对于样本\(x\)，因为我们已经假设特征之间是独立的，则可以计算出样本概率：

\(\displaystyle
p(x)=\prod_{j=1}^{n}p(x_j;\mu_j,\sigma_j^2)
\)

当\(p(x)<\epsilon\)时，我们认为该样本是异常的。

多变量高斯分布

多变量高斯分布可以发现不同特征间的关联，但是计算开销更高。

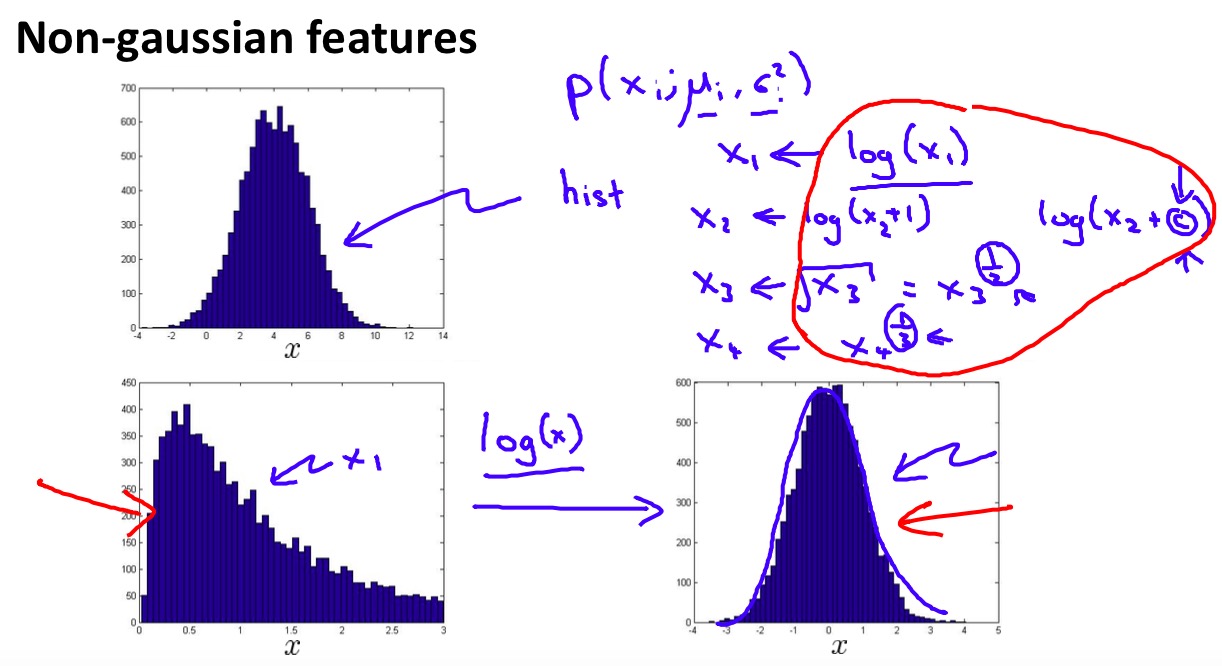
特征变换

那么，如果某个特征不服从高斯分布该怎么办呢？答案是对特征进行变换，让新特征的分布更像高斯分布。

---

F₁ score

到这里为止我们都回避了一个重要的问题，如何选定合适的\(\epsilon\)？

和之前的各种学习算法选择参数的方法相同，我们可以在验证集中对参数进行挑选。那么，该如何衡量参数的好坏呢？准确率在异常检测的问题中是不可行的，异常检测问题明显属于类不平衡问题，即属于正常类别的样本要远远多于属于异常类别的样本，在这样的问题中准确率无法很好的衡量算法的效果，试想如果简单预测所有样本都为正常样本，算法仍然可以获得很好的准确率。因此，和其他类不平衡的分类问题一样，我们使用F₁ score来作为算法的评估标准。

F₁ score实际上另外两种评价标准：精度（precision）和召回率（recall）的一种结合使用。精度是算法精确性的度量（即标记为正类的元组中实际为正类的元组所占的百分比），召回率是算法完全性的度量（即正元组被标记为正的百分比）。

\(
\displaystyle precision=\frac{TP}{TP+FP} \\
\displaystyle recall=\frac{TP}{TP+FN}=\frac{TP}{P}
\)

两种度量存在Trade off的关系，有可能通过降低其中一个为代价来提高另一个：

F₁ score是精度和召回率的调和均值，它赋予精度和召回率相等的权重：

\(
\displaystyle F_1 = \frac{2 \times precision \times recall}{precision + recall}
\)

在异常检测算法中，我们通过在验证集上尝试\(\epsilon\)，并通过F₁ score对模型进行评估来得到较好的参数\(\epsilon\)。

---

参考资料

• Machine Learning by Andrew Ng on Coursera
• 《数据挖掘 概念与技术（第三版）》Jiawei Han, Micheline Kamber, Jian Pei