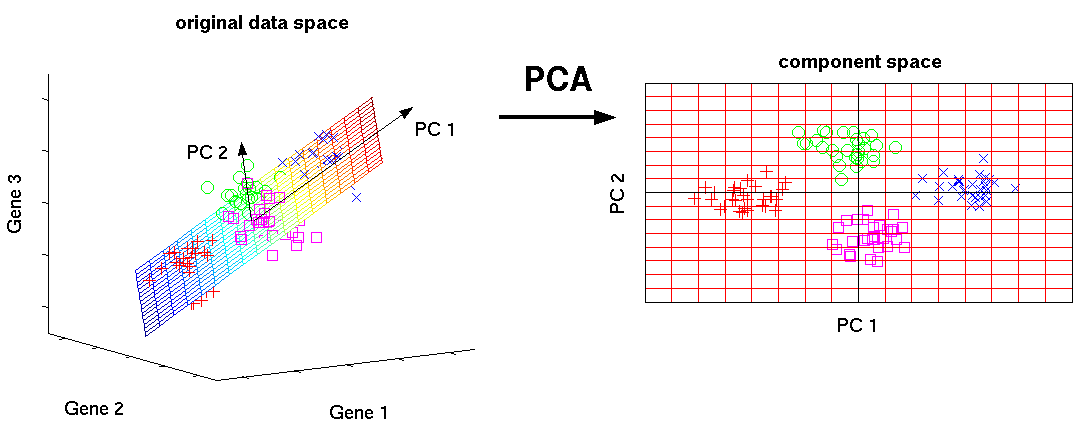
主成分分析（PCA）是一种通常用来做数据降维的非监督学习算法，下图是数据降维的直观说明：
Principal Component Analysis
在PCA中，我们将每个样本看做特征线性空间中的一个向量，左图代表具有三个特征的样本（处于三维空间中，每个特征代表一个维度），通过寻找空间中样本的主成分PC1、PC2，以此建立新的二维线性空间来完成3D到2D的降维。
数据降维
数据降维的常见使用场景如下：
- 发掘样本间隐藏的联系
- 去除样本中冗余的属性和噪声
- 对样本进行可视化（3维以上的数据难以可视化）
- 减少数据容量、加速学习速度
主成分分析（PCA）
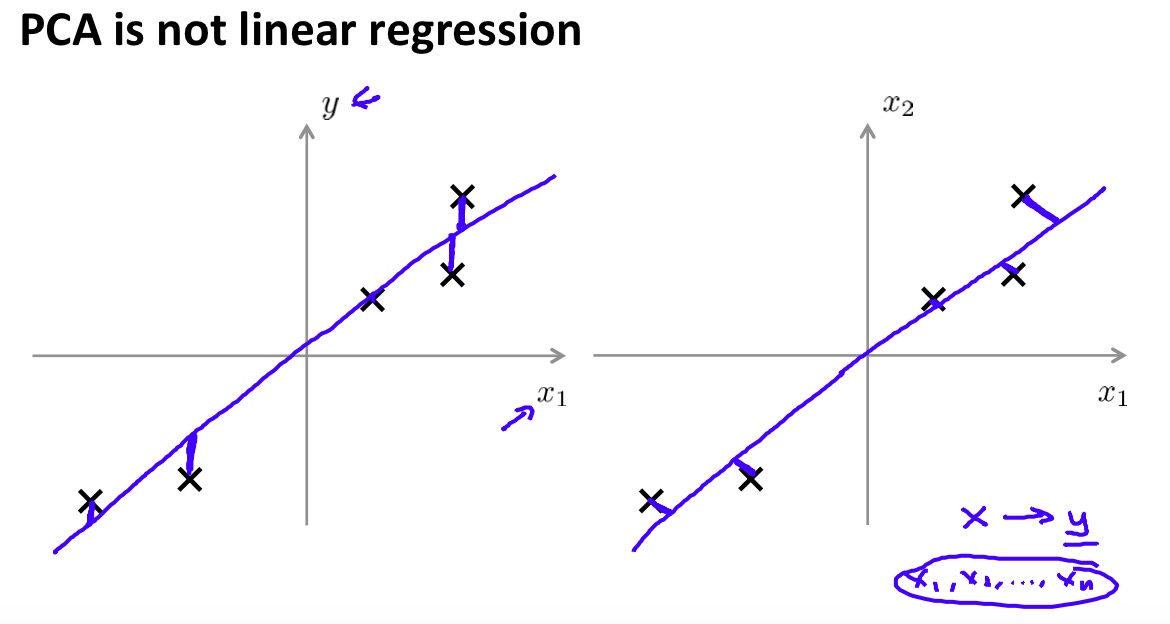
PCA是一种常见的数据降维算法，其核心思想非常的简单：寻找一个低维的超平面，使所有样本和其在该低维超平面上的投影间的距离和最小，如下图：
PCA is not linear regression
Ng在这页slide上着重强调了PCA和线性回归的区别：线性回归的Cost function重点在回归值和真实值的误差，而PCA着重样本与超平面的投影距离。
数据预处理
在使用PCA算法之前，和之前讲过的几种学习算法相似，我们首先需要对样本进行预处理，预处理过程依然是feature scaling/mean normalization的方法，对于输入样本\(x^{(1)},x^{(2)},\dots,x^{(m)}\)，求取每个属性的平均值：
\mu_j=\frac{1}{m} \sum_{i=1}^{m} x_j^{(i)}
\)
然后对所有样本的各个属性进行替换：
x_j^{(i)}=\frac{x_j^{(i)}-\mu_j}{s_j}
\)
其中\(s_j\)表示属性\(x_j\)的标准差。
PCA算法
Ng对PCA算法的讲解非常的概要，都浓缩在这个slide里：
Principal Component Analysis (PCA) algorithm summary
算法主要依赖于SVD矩阵分解：
- 首先计算出协方差矩阵（covariance matrix）\(\Sigma\)
- 对协方差矩阵执行SVD矩阵分解，得到矩阵\(U\ S\ V\)（SVD矩阵分解详见后文）
- 取矩阵\(U\)的前\(k\)个向量作为新线性空间的一组基向量\(U_{reduce}\)
- 为什么要计算协方差矩阵？
- 为什么要对协方差矩阵执行SVD分解？
- 分解后的结果代表什么？
- Machine Learning by Andrew Ng on Coursera
- Mining Massive Datasets by Jure Leskovec, Anand Rajaraman, Jeff Ullman on Coursera
- Pattern recognition, CS, Nanjing University Spring, 2014, Jianxin Wu
- Wikipedia
数据维度转换
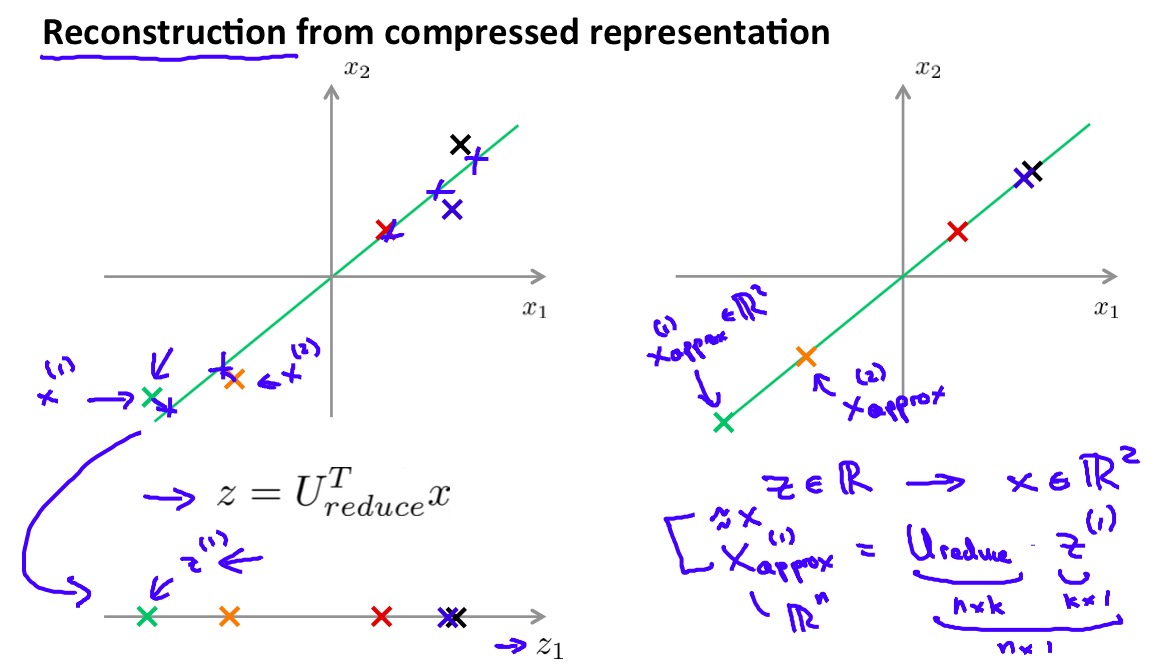
得到低维的线性空间后，降维的工作实际上是将原来线性空间中的向量投影到低维线性空间中，对于样本\(x^{(i)}\)，映射到低维空间投影\(z^{(i)}\)：
z^{(i)}=U_{reduce}^T\times x^{(i)}
\)
类似的，将降维后的样本映射回原空间如下：
x_{approx}^{(i)}=U_{reduce}\times z^{(i)}
\)
这里使用\(x_{approx}\)是因为在降维后损失了一定信息，即使映射回原空间也只是原先样本的近似而无法准确的还原。
向量映射
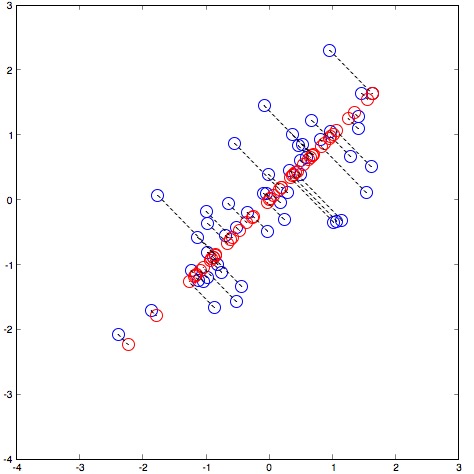
下图是一个示例，将2维数据降维到1维（直线）后的映射关系，红色代表数据在低维的投影：
Dimensionality Reduction
SVD矩阵分解
虽然在看完Ng的课程后已经足够编写和使用PCA进行数据降维的工作了，但我们也可以看到Ng对PCA背后的数学原理省略了相当多的内容：
实际上这些内容中包含了相当多的数学工作，应该是出于课程内容难度的考量，Ng没有选择详细的讲解这些内容，如果只是使用PCA，Ng所讲的内容也已经足够了。关于主成分分析的更多原理，参见这里，还有SVD的内容，在这里（真希望自己当年有好好学线性代数ToT）。
不过，为了对PCA过程有个更好的感觉，至少我们需要对于SVD（奇异值分解）的一些基本性质有所了解。
对于任意\(m\times n\)的输入矩阵\(A\)，SVD分解结果为：
A_{[m\times n]}=U_{[m\times r]}\ \Sigma_{[r\times r]}\ (V_{[n\times r]})^T
\)
分解结果中\(U\)为左奇异向量（left singular vectors），\(\Sigma\)为奇异值矩阵，\(V\)为右奇异向量（right singular vectors）。
矩阵\(U,\ V\)中的列向量均为正交单位向量，而矩阵\(\Sigma\)为对角阵，并且从左上到右下以递减的顺序排序。引用维基百科中的解释：
奇异值分解在统计中的主要应用为主成分分析（PCA）。数据集的特征值（在SVD中用奇异值表征）按照重要性排列，降维的过程就是舍弃不重要的特征向量的过程，而剩下的特征向量张成空间为降维后的空间。
SVD的另一种常见的应用场景在推荐系统中，以后有机会再写。
选择合适的k
在数据降维中一个重要的问题是如何选择合适的\(k\)，即应该降到什么维度。一个典型的选择方式是“对数据降维，并且保留原数据99%的方差”，方差被认为是特征中包含信息多少的度量（有时被称为能量energy），形式化为选择最小的\(k\)，满足：
\frac{\frac{1}{m}\sum_{i=1}^{m}\left \| x^{(i)}-x_{approx}^{(i)} \right \|^2}{\frac{1}{m}\sum_{i=1}^{m}\left \| x^{(i)} \right \|^2}\le 0.01
\)
但是从小到大尝试\(k\)再计算上式验证似乎太复杂了，实际上我们可以利用SVD分解得到的矩阵\(S\)，把这个上面的过程简化为：
\frac{\sum_{i=1}^kS_{ii}}{\sum_{i=1}^mS_{ii}}\ge0.99
\)
美好的SVD，不是么…
举个栗子
这次Ng的实验中展示了一个使用PCA作为人脸检测预处理的例子，使用的人脸数据看上去是这样的：
Original faces
每一个人脸图像的分辨率为36*36，每个像素作为一个灰度特征值则我们将每个人脸图片作为一个1024维的样本进行处理，进行PCA降维至100维，映射回原始空间进行可视化得到了下面的效果：
Recovered faces
可以观察到非常有趣的结果，虽然经过PCA数据维度降低了非常多，但是人脸的五官还是基本保留了下来（这也形象的说明了“主成分”的意义），对后续的学习算法是一个很好的加速。