这已经是我第三次学习K-means算法了，K-means算法应该说不是一个复杂的算法，就做一个相对比较简单的记录吧。

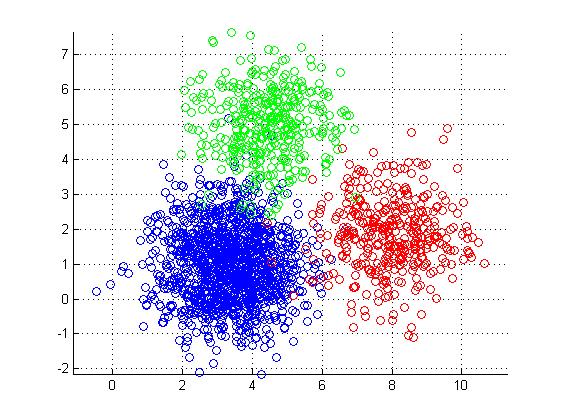
K-means算法是Ng引入的第一个非监督学习算法，所谓非监督学习，就是在没有人工标注的label \(y^{(i)}\)的情况下对输入数据\(x^{(i)}\)进行学习。K-means是一种聚类算法，最终获得的效果是将数据集划分为K个类别。

---

K-means

以欧式空间为例，K-means算法的思想是为每一个类寻找空间中的中心点（centroid），使得所有的点距离自己所属类别的中心点的距离和相对较小。若输入有\(m\)个样本\(x^{(i)}\)，计算得\(k\)个类别，每个类别的中心点编号为\(\mu_k\)，对于第\(i\)个样本，其类别编号为\(c^{(i)}\)，则K-means算法的优化目标可以表示如下：

\( \displaystyle
J(c^{(1)},\dots,c^{(m)},\mu_1,\dots,\mu_K)=\frac{1}{m}\sum_{i=1}^{m}\left \| x^{(i)}-\mu_{c^{(i)}} \right \|^2
\)

式子相当直观，K-means算法为了最小化优化目标，不断的重复Cluster assignment和Move centroid两步直到收敛，如下：

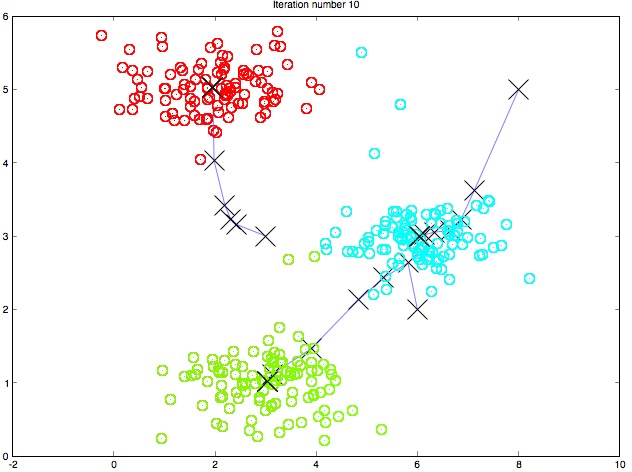
通过一幅图来观察迭代过程中每次迭代产生的中心点的变化如下：

---

随机初始化

K-means算法通过随机执行K个中心点对算法进行初始化，由于K-means算法存在局部最优解，因此不同的初始化会导致不同的聚类结果，因此实践中通常多次执行K-means算法（随机初始化）并选择最优的聚类结果（\(J(c^{(1)},\dots,c^{(m)},\mu_1,\dots,\mu_K)\)最小）。

---

选择K

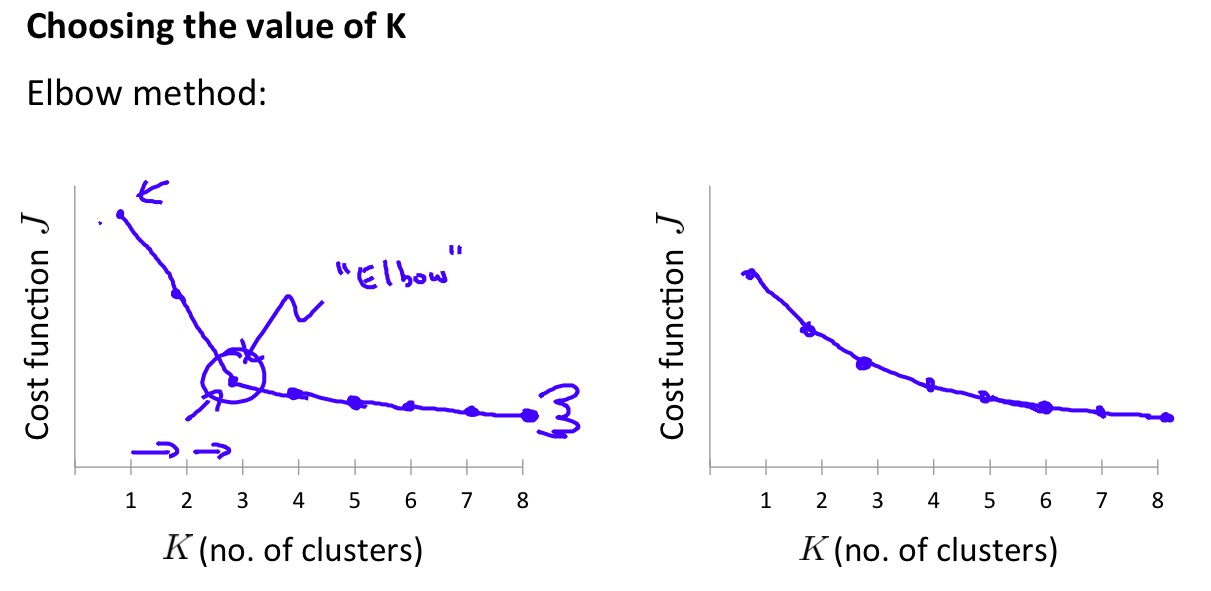
在K-means算法中一个重要的问题是如何选择合适的K，Ng讲了一种Elbow method可以选择合适的K：

但是，如上图右侧的示意图，Elbow method并不总是有效，在大部分情况下仍然需要人为的指定K的值，因为我们在运行K-means算法时通常对结果的类别会有一定的预期，所以这样做也是可行的。

---

举个栗子

Ng课后作业中有一个很有意思的例子：使用K-means算法做图像压缩。

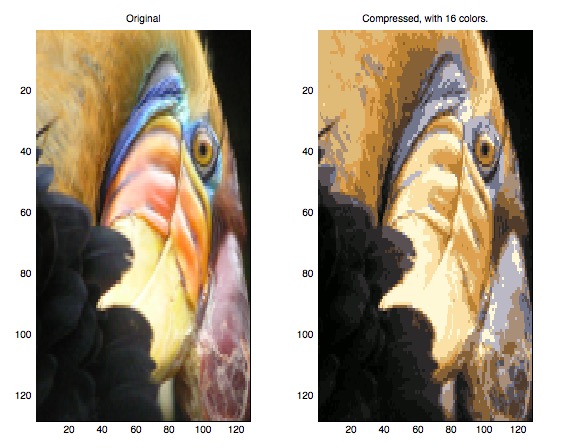
其做法非常简单，在图像的颜色RGB空间（三维）中做聚类，获得16个类，将中心点作为新的16个颜色对原图像中的颜色进行替换，效果还不错:

在我机器上产生了奇怪的拉伸效果，其实这是一只鸟…

---

参考资料

• Machine Learning by Andrew Ng on Coursera