Fanyu Kong

good good code, day day up!

Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

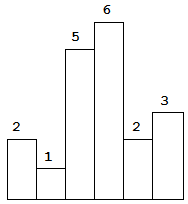
histogram

Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

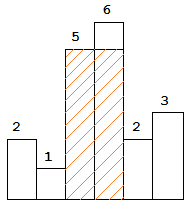
histogram_area

The largest rectangle is shown in the shaded area, which has area = 10 unit. For example, Given height = [2,1,5,6,2,3], return 10.

题目链接在这里

O(n2)

这道题目最为朴素的解法时间复杂度为O(n2)，简单的枚举所有的点对作为区间的起点和终点，并计算所围成的最大矩形面积并找到最大值即可。 但是显然，这样做太低效了。

O(nlogn)

更近一步，我们可以得到一个基于分治思想时间复杂度为O(nlogn)解法： 对于任何一个区间，我们首先找到这个区间中的最低点，则这个区间中最大的矩形面积为如下三种情况的最大值：

  1. 最低点左边区间中的最大矩形面积
  2. 最低点右边区间中的最大矩形面积
  3. 最低点作为矩形的高所围成的矩形面积

这样我们就得到了一个分治解法，如下：

class Solution
{
public:
    int largestRectangleArea(vector<int> &height)
    {
        return maxArea(height, 0, height.size());
    }
 
private:
    int maxArea(vector<int> &height, int l, int r)
    {
        if (l >= r) {
            return 0;
        }
 
        int min = height[l];
        int index = l;
 
        if (l >= r) {
            return 0;
        }
 
        for (int i = l; i < r; ++i) {
            if (height[i] < min) {
                min = height[i];
                index = i;
            }
        }
 
        int left = maxArea(height, l, index);
        int right = maxArea(height, index + 1, r);
        int ans = (r - l) * min;
 
        if (left > ans) {
            ans = left;
        }
 
        if (right > ans) {
            ans = right;
        }
 
        return ans;
    }
};

O(nlogn)的解法对这道题目来说还不够好，更悲剧的上面的O(nlogn)解法存在最差情况：当输入序列为递增序列时，这个解法会退化为O(n2)，这是我们不能够接受的。

O(n)

O(n)算法相比上面两种方法来说更加的巧妙，其基本思路是：对输入序列中的每一项，都得到以该项作为最低点所能围成的最大矩形面积，并得到其中的最大值作为解。 这个思路的正确性是显然的，为了有效的实现这个思路，在过程中维护了一个存放序列索引的栈，对输入序列依次遍历：

  1. 当输入项大于栈顶索引对应的输入项时，将输入项索引入栈
  2. 当输入项小于栈顶索引对应的输入项时，不断出栈栈顶索引直到输入项大于栈顶索引对应的输入项。同时，对每个出栈的栈顶索引：以该索引对应的输入项为最低点的矩形的左边界为栈内前一个元素–新的栈顶（因为栈内元素的递增的），而右边界就是当前正在遍历的输入项，因此可以在O(1)的时间内计算出这个矩形的面积。
  3. 当遍历结束后如果栈不为空，则对栈依次出栈并执行步骤2

看下代码就明白了：

class Solution
{
public:
    int largestRectangleArea(vector<int> &height)
    {
        return getMaxArea(height, height.size());
    }

private:
    // The main function to find the maximum rectangular area under given
    // histogram with n bars
    // http://www.geeksforgeeks.org/largest-rectangle-under-histogram/
    int getMaxArea(vector<int> &hist, int n)
    {
        // Create an empty stack. The stack holds indexes of hist[] array
        // The bars stored in stack are always in increasing order of their
        // heights.
        stack<int> s;

        int max_area = 0; // Initalize max area
        int tp;  // To store top of stack
        int area_with_top; // To store area with top bar as the smallest bar

        // Run through all bars of given histogram
        int i = 0;
        while (i < n)
        {
            // If this bar is higher than the bar on top stack, push it to stack
            if (s.empty() || hist[s.top()] <= hist[i])
                s.push(i++);

            // If this bar is lower than top of stack, then calculate area of rectangle
            // with stack top as the smallest (or minimum height) bar. 'i' is
            // 'right index' for the top and element before top in stack is 'left index'
            else
            {
                tp = s.top();  // store the top index
                s.pop();  // pop the top

                // Calculate the area with hist[tp] stack as smallest bar
                area_with_top = hist[tp] * (s.empty() ? i : i - s.top() - 1);

                // update max area, if needed
                if (max_area < area_with_top)
                    max_area = area_with_top;
            }
        }

        // Now pop the remaining bars from stack and calculate area with every
        // popped bar as the smallest bar
        while (s.empty() == false)
        {
            tp = s.top();
            s.pop();
            area_with_top = hist[tp] * (s.empty() ? i : i - s.top() - 1);

            if (max_area < area_with_top)
                max_area = area_with_top;
        }

        return max_area;
    }
};

参考资料

  1. Largest Rectangular Area in a Histogram

Comments