字符串匹配的后缀算法

September 8, 2015

字符串匹配问题是算法领域的经典问题，C/C++中常用的strstr函数就是这个问题的定义:

const char* strstr( const char* str, const char* target ); char* strstr( char* str, const char* target );

Finds the first occurrence of the byte string target in the byte string pointed to by str. The terminating null characters are not compared.

在目标字符串str中寻找是否存在子串target，字符串str的长度为\(n\)，target的长度为\(m\)。这个问题最为人所熟知的算法应该是KMP（Knuth-Morris-Pratt）算法，其时间复杂度为\(O(n)\)，想法非常酷。

但是，Can we do better？

如我们所知的，KMP算法是一个前缀匹配算法，因为从前向后匹配比较自然也比较保守，所以很难突破\(O(n)\)的天花板，但后缀匹配算法没有这样的限制，比如BM（Boyer-Moore）算法就实现了\(O(n/m)\)的最好情况时间复杂度，最差情况时间复杂度为\(O(n)\)，虽然与KMP算法相比BM算法的最差情况具有更大的常数，但是在实际使用中（自然语言）BM算法往往具有优于KMP的性能表现，并且模式串越长性能表现越好。我不想浪费时间搬运现有的算法资料，也不认为我可以讲的更好，所以在本文中会直接给出相应算法的链接，比如BM算法。

在BM算法横空出世以后，人们惊讶的发现原来这个问题还可以这么玩！于是非常多的算法研究人员对BM算法进行了研究并提出了各种各样的改进方案，Horspool在1980年提出的Boyer-Moore-Horspool算法就是一种基于BM的改进（或者应该说是简化更合适）：Horspool只使用了BM算法中的坏字符规则（基于窗口的最右字符），并且在实验中验证了其实际使用中的性能甚至要优于BM算法。需要注意的是这并不能代表BM算法中的好字符规则是毫无意义的，好字符规则保证了BM算法具有\(O(n)\)的最差情况时间复杂度，而Horspool的最差情况时间复杂度为\(O(nm)\)，只是在实际使用中很难出现而已。

下图是对一些字符串匹配算法进行测试的结果：

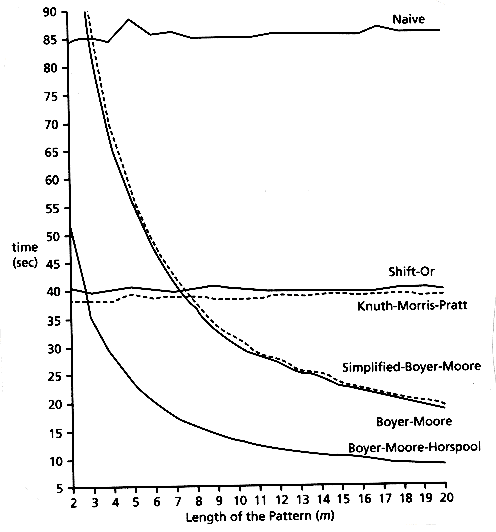
可以看到，抛弃了好字符规则的Horspool具有很好的运行效果。需要注意的是，这些实验是在自然语言（ASCII）中测试得到的，在小字符集的字符串（比如DNA序列）可能会得到不同的结果。

Sunday在1990年提出了另一个基于Boyer-Moore算法的改进（简化）的算法，通常称为Sunday算法，同样只使用坏字符规则，和Horspool算法的思路一脉相承，不同点在于：Horspool算法使用窗口的最右字符，而Sunday更激进，使用窗口后的第一个字符来计算偏移量，获得了更快的窗口移动速度，代码如下：

#include <string.h>

const int CSIZE = 256; // size of whole character set

/**
 * preprocessing step for sunday algorithm
 * calculate bad-character shift table
 */
static void prepare(const char *target, int m, int bad_table[])
{
    for (int i = 0; i < CSIZE; ++i) {
        bad_table[i] = m + 1;
    }

    for (int i = 0; i < m; ++i) {
        bad_table[target[i]] = m - i;
    }
}

/**
 * strstr function implemented using sunday algorithm
 */
const char* strstr_sunday(const char* str, const char* target)
{
    if (NULL == str || NULL == target) {
        return NULL;
    }

    int n, m;
    n = strlen(str);
    m = strlen(target);

    if (!m) return str;
    if (!n) return NULL;

    /* preprocessing */
    int bad_table[CSIZE];
    prepare(target, m, bad_table);

    /* searching */
    int i = 0;
    while (i <= n - m) {
        if (memcmp(target, str + i, m) == 0) {
            return str + i;
        }

        i += bad_table[str[i + m]];
    }

    return NULL;
}

参考资料

《Algorithms, Part II》on Coursera
The Boyer-Moore-Horspool Algorithm

Fanyu Kong

字符串匹配的后缀算法

参考资料

Comments