有向图强连通分支：Kosaraju’s algorithm

March 16, 2015

有向图强连通分支算是个基础算法，不过总是忘记，写下来备忘。

无向图强连通分支非常简单，使用图的遍历算法（DFS或BFS）即可，而有向图的强连通分支计算则要复杂一些，Kosaraju’s algorithm实现了$O(n+m)$时间复杂度的有向图强连通分支算法。

算法的核心思想在于：从有向图中任何一个点出发做DFS，必然能从图中“拖”出一个点集，和无向图中不同的是，这个点集不一定构成强连通分支，但是如果我们能通过一个合适的顺序进行DFS（“sink” vertex），则可以依次把每一个强连通分支“拖”出来，得到正确的结果，那么算法的要点则在于如何寻找这个合适的顺序。

算法通过两次DFS来求解，步骤如下：

对原图$G$做反转(reverse)操作，即将所有有向边逆置，得到图$G^{rev}$
在图$G^{rev}$上做后序的DFS，得到点遍历顺序
按照上一步中得到的遍历顺序，从大到小在原图$G$中通过DFS依次“拖”出强连通分支

运行过程如下图例，$f(v)$代表点在$G^{rev}$的遍历结束时间，从9号点开始DFS。

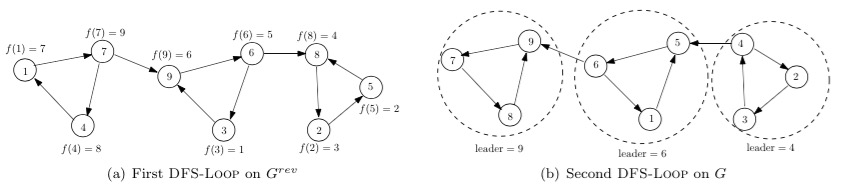
Example execution of the strongly connected components algorithm.

记得刚学习这个算法时一直有的一个疑惑：为什么在第一遍DFS时一定要在图$G^{rev}$上做么？难道不能通过在原图$G$上DFS的顺序从小到大的进行第二次DFS么？仔细研究算法正确性的证明，不难发现这个想法是错误的。

该算法正确性证明的核心在于对于图$G$中任意两个相邻的强连通分支$C_1$和$C_2$且存在边$(i,j)$满足$i \in C_1 \land j \in C_2$（在强连通分支的DAG中方向为$C_1 \to C_2$），可以证明：

\[\max_{v\in C_1}f(v) < \max_{v\in C_2}f(v)\]

$f(v)$代表点在$G^{rev}$的遍历结束时间，因此，在图G中具有最大$f(v)$的点一定为“sink” vertex。

那么现在来看看之前的想法错在哪里了，令$f’(v)$代表点在$G$的遍历结束时间，如果按照从小到大的顺序在$G$可以依次”拖”出强连通分支，则我们需要证明(强连通分支$C_1$和$C_2$的定义同上)：

\[\min_{v\in C_1}f(v) > \min_{v\in C_2}f(v)\]

显然这是不对的…反例见下图中强连通分支{9，6，3}和{8，5，2}，$f’(3)=1$比{8，5，2}中的完成时间都要小，如果从该点开始“拖”强连通分支得到的是错误的结果{9，6，3，8，5，2}。

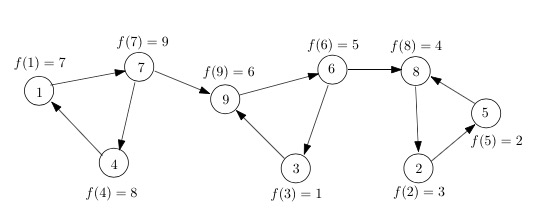
所以$G^{rev}$的计算是必不可少的。

代码如下，采用递归实现DFS，在实际使用中容易造成栈溢出，修改为非递归实现即可。

#include <vector>
#include <list>
#include <stack>
#include <iostream>
#include <fstream>
#include <cassert>
#include <unordered_map>
#include <algorithm>

using namespace std;

class Graph
{
public:
    Graph(int n)
    {
        _storage.resize(n);
    }

    void addVertex()
    {
        _storage.push_back(list<int>());
    }

    void addEdge(int vertex, int adjacent)
    {
        _storage[vertex].push_back(adjacent);
    }

    int vertices()
    {
        return _storage.size();
    }

    int edges()
    {
        int count = 0;
        for (int i = 0; i < vertices(); ++i) {
            count += _storage[i].size();
        }
        return count;
    }

    list<int> &edges_for_vertex(int vertex)
    {
        return _storage[vertex];
    }

private:
    vector<list<int> > _storage;
};

class SCC
{
public:
    vector<int> calculateSCC(Graph &g)
    {
        int n = g.vertices();
        Graph g_rev(n);

        for (int v = 0; v < n; ++v) {
            list<int> &edges = g.edges_for_vertex(v);
            for (int u : edges) {
                g_rev.addEdge(u, v);
            }
        }

        assert(g.edges() == g_rev.edges());

        stack<int> s;
        vector<bool> map(n, false);

        // first pass
        for (int i = 0; i < n; ++i) {
            if (!map[i]) {
                dfs_order(g_rev, i, s, map);
            }
        }

        vector<int> ssc(n, -1);

        // second pass
        while (!s.empty()) {
            int i = s.top();
            s.pop();

            if (ssc[i] < 0) {
                dfs_ssc(g, i, i, ssc);
            }
        }

        return ssc;
    }

private:
    void dfs_order(Graph &g, int v, stack<int> &s, vector<bool> &map)
    {
        map[v] = true;

        list<int> &edges = g.edges_for_vertex(v);
        for (int u : edges) {
            if (!map[u]) {
                dfs_order(g, u, s, map);
            }
        }

        s.push(v);
    }

    void dfs_ssc(Graph &g, int v, int leader, vector<int> &ssc)
    {
        ssc[v] = leader;

        list<int> &edges = g.edges_for_vertex(v);
        for (int u : edges) {
            if (ssc[u] < 0) {
                dfs_ssc(g, u, leader, ssc);
            }
        }
    }
};

vector<int> rankSCC(vector<int> &scc)
{
    unordered_map<int, int> count;

    for (int i = 0; i < scc.size(); ++i) {
        if (count.find(scc[i]) != count.end()) {
            count[scc[i]] += 1;
        } else {
            count[scc[i]] = 1;
        }
    }

    vector<int> rank;
    for (auto it = count.begin(); it != count.end(); ++it) {
        rank.push_back(it->second);
    }

    sort(rank.begin(), rank.end());
    return rank;
}

int main(int argc, char *argv[])
{
    ifstream fin("SCC.txt");


    int n = 875714;
    Graph graph(n);

    while (fin) {
        int s = 0, t = 0;
        fin >> s >> t;
        if (s != 0 && t != 0) {
            graph.addEdge(s - 1, t - 1);
        }
    }

    cout << graph.edges() << " lines loaded." << endl;

    SCC solver;
    vector<int> scc = solver.calculateSCC(graph);
    vector<int> rank = rankSCC(scc);

    int total = 0;
    for (int i = 0; i < rank.size(); ++i) {
        total += rank[i];
    }
    assert(total == n);

    for (int i = rank.size() - 1; i >= rank.size() - 5; --i) {
        cout << rank[i] << ',';
    }
    cout << endl;

    return 0;
}

好吧，我承认我就是为了凑数的…

参考资料

Algorithms: Design and Analysis, Part 1 by Tim Roughgarden on Coursera

Fanyu Kong

有向图强连通分支：Kosaraju’s algorithm

参考资料

Comments