Machine Learning小结(2)：SVM

继续总结Ng的课程内容，这次是SVM。Ng在课程中说：

Most people consider the SVM to be the most powerful “black box” learning algorithm.

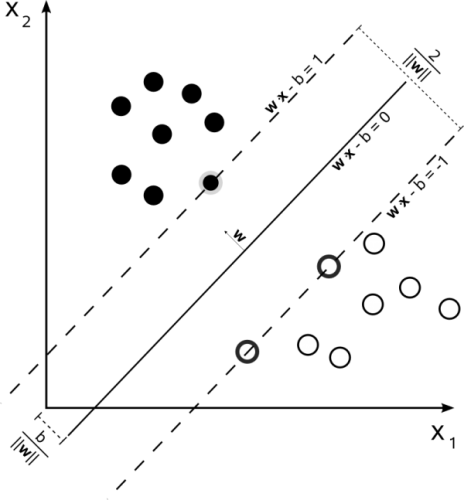
在实践中，SVM也的确是一种非常流行的“黑盒”学习算法，下图为SVM标志性的概念图：

Support Vector Machine

SVM with hard constraints

SVM也是一种线性模型，为了与之前讲的几个线性模型分类器一致，Ng在课程中并没有使用SVM研究中所常用的符号（如上图），而大部分沿用了之前课程中的符号：

训练集：\(x\)，其中\(x^{(i)}\)为第\(i\)个训练样本，\(x_j^{(i)}\)代表该样本的第\(j\)个属性；\(y^{(i)}\)表示其对应的正确的回归值
\(\theta\)表示SVM训练得到的参数，也可以理解为超平面的一个法向量

首先来看不允许发生错误分类的条件下SVM是如何工作的，这往往被称为“SVM with hard constraints”。

\( \displaystyle
\begin{aligned}
&\min _{\theta} \frac{1}{2} \sum _{j=1}^{n} \theta_{j}^{2} \\
s.t. \ &\theta^{T}x^{(i)} \ge 1 \qquad &if \ y^{(i)}=1 \\
&\theta^{T}x^{(i)} \le -1 \qquad &if \ y^{(i)}=0
\end{aligned}
\)

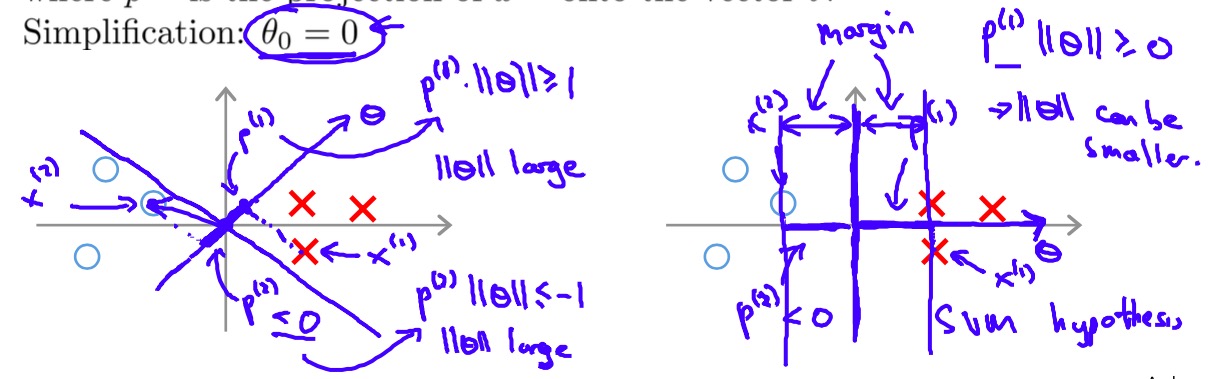
这个式子看上去很难理解，和之前优化Cost function的套路不同，这优化的是个啥？看Ng慢慢展开：\(\frac{1}{2} \sum _{j=1}^{n} \theta_{j}^{2}=\frac{1}{2} {\left \| \theta \right \|}^2\)，优化目标变成了最小化向量\(\theta\)的长度？那岂不是可以一直优化到无穷小？别忘了还有约束条件，如果我们将训练样本\(x^{(i)}\)看做一个向量，那么\(\theta^{T}x^{(i)}\)即为向量\(\theta\)和训练样本的内积，再写一步\(\theta^{T}x^{(i)}=p^{(i)}\cdot{\left \| \theta \right \|}\)，\(p^{(i)}\)为训练样本\(x^{(i)}\)在\(\theta\)上的投影，则我们得到了下面的优化目标：

\( \displaystyle
\begin{aligned}
&\min _{\theta} \frac{1}{2} \sum _{j=1}^{n} \theta_{j}^{2}=\frac{1}{2} {\left \| \theta \right \|}^2\\
s.t. \ &p^{(i)}\cdot{\left \| \theta \right \|} \ge 1 \qquad &if \ y^{(i)}=1 \\
&p^{(i)}\cdot{\left \| \theta \right \|} \le -1 \qquad &if \ y^{(i)}=0
\end{aligned}
\)

上面的式子比起之前的形式更清楚的说明了SVM到底在做什么：通过最小化\(\frac{1}{2} {\left \| \theta \right \|}^2\)，SVM实际上是在寻找合适的\(\theta\)使得在各个训练样本\(x^{(i)}\)上获得更大的投影来满足限制条件，这也对应了更大的margin（所以SVM也叫Large margin classifier）,简单来说，SVM的目标不仅使找到可以分开正反类别的超平面，而且希望能找个“最好”的超平面，即距离正反类别样本距离最远的超平面，如下图：

Larger margin

错误惩罚

为了避免过拟合，我们需要容忍SVM训练中有一定的错误，和之前的思路相似，错误会造成Cost，因此需要在我们的优化目标中加入错误产生的代价：

\( \displaystyle
\min _{\theta} C \sum_{i=1}^m \left[ y^{(i)}cost_1(\theta^{T}x^{(i)}) + (1-y^{(i)})cost_0(\theta^{T}x^{(i)}) \right] + \frac{1}{2} \sum _{j=1}^{n} \theta_{j}^{2} \\
\)

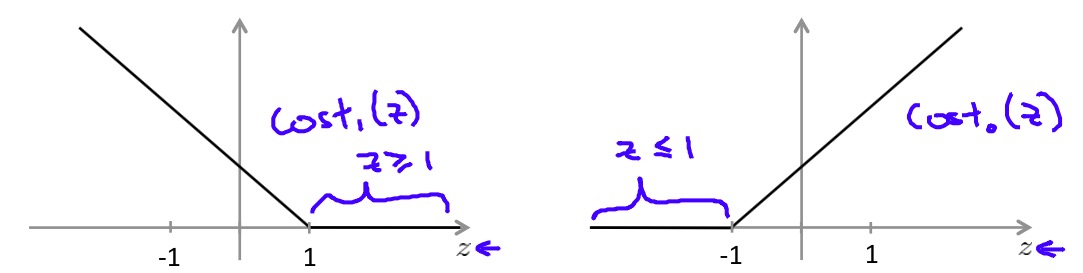
其中\(C\)是惩罚系数，后面的两项中\(cost_1\)和\(cost_0\)实际上是Hinge loss函数：

Hinge Loss

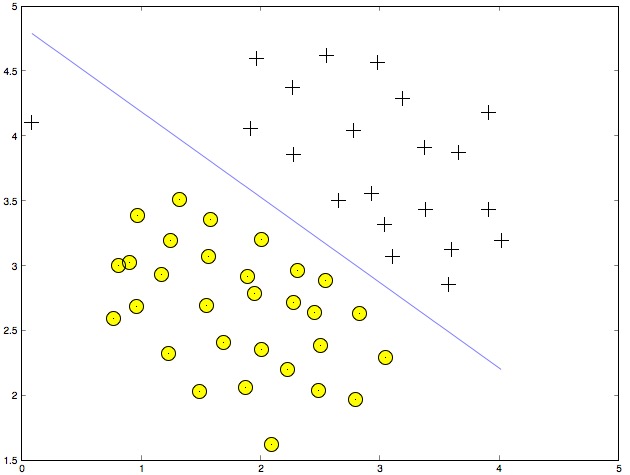
到这里我们已经得到了线性核的SVM，训练个线性分类器看看效果：

Linear Kernel

Kernel

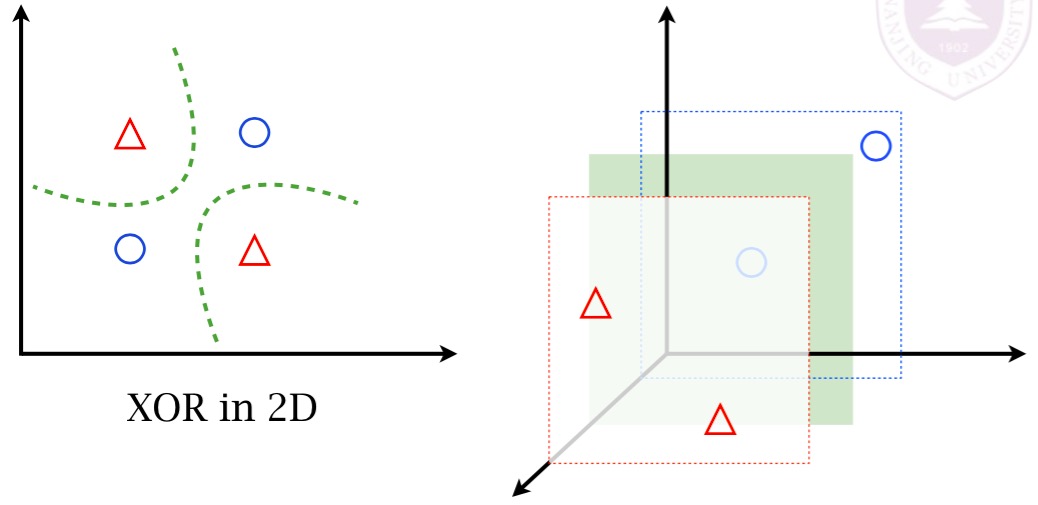
SVM的核（Kernel），本质上是把低维空间的样本映射到高维空间，在低维空间线性不可分的样本在高维空间可能会变为线性可分的，见下图：

Linearity v.s. dimensionality

在线性回归和逻辑回归中，我们通过添加高次项的方法将样本从低维空间映射到高维空间，在SVM中通过Kernel来完成映射，如果不使用任何Kernel，则称该SVM是线性核（Linear Kernel）。

核的作用十分简单，通过将所有的\(m\)个训练样本作为landmarks \(l^{(i)}\)，从而将样本映射到\(m\)维空间，特征为\(f_i=similarity(x,l^{(i)})\)，确实是映射到了很高维的空间有木有…

高斯核（RBF）是一种常用的SVM Kernel:

\( \displaystyle
f_i=similarity(x,l^{(i)})=\exp\left( -\frac{\left \| x-l^{(i)} \right \|^2}{2\sigma^2} \right)
\)

在使用Gaussian kernel时要注意不要忘记做feature scaling！否则会导致规模较小的特征被忽略，相信这不会是你想要的结果。
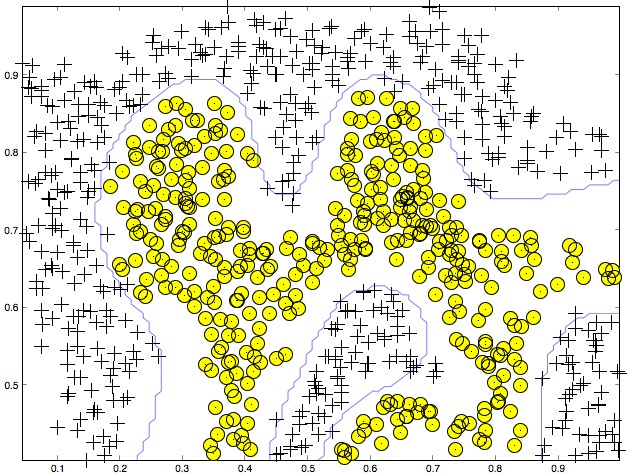
直到最后Ng也没有将SVM具体是如何运行的，只是说虽然特征维度很高，但只要Kernel满足“Mercer’s Theorem”，SVM的运算过程是非常有效的，看来SVM确实很适合被当做“黑盒”来使用…训练一个高斯核SVM分类器看看效果：

Gaussian kernel

参数选择和交叉验证

在实际使用SVM时，以Gaussian kernel为例，需要选择合适的参数\(C\)和\(\sigma\)：

SVM parameters

具体的建议Ng已经给出了，我们需要在实际的过程中在交叉验证集上选择合适的参数，最终在测试集上检验模型的泛化误差。因为如果在测试集上选择参数再测试泛化误差，本身参数就是针对测试集优化，这样做使得泛化误差的检验变得不公平，所以参数的选择必须在独立的交叉验证集中进行。

模型选择

因为SVM是Ng课程中讲的最后一个监督学习算法，所以Ng在之后还给出了对问题如何选择合适的学习模型的建议：

Model selection

在另一门课程mmds中，也给出了SVM和决策树模型之间的选择建议，一并贴出留念：

SVM vs Decision Tree

但是这些只能对选择模型做出一定的参考，而不能仅凭特征数量来选择模型，如俞扬老师说：

简单以样本和特征数量来选择学习器不太合适吧，特征性质和样本分布更重要，是否使用核方法要看数据的可分性，如果特征远多于样本也许该先尝试特征选择和抽取

在实际应用中模型的选择还是需要更多的考量和经验。

参考资料

Machine Learning by Andrew Ng on Coursera
Mining Massive Datasets by Jure Leskovec, Anand Rajaraman, Jeff Ullman on Coursera
Data Mining for M.Sc. students, CS, Nanjing University Fall, 2013, Yang Yu

kongfy

发表于

2014-11-18

kongfy 分类：机器学习 | 2014-11-18